THE FORM OF THE ACCELERATION POTENTIAL

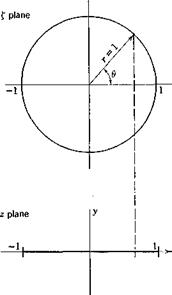
A two-dimensional airfoil is conveniently treated by conformal mapping. The transformation between the complex numbers z and £

maps a circle of unit radius on the £ plane into a straight-line segment from x = — 1 to x = 1 on the real axis of the z plane (Fig. 13.2). A point with polar coordinates r (= 1) and в on the circle corresponds to the point x = cos 0, у = 0 on the line segment. The space outside the circle maps into the whole z plane, and that inside the circle is mapped into a second sheet of Riemann surface.

According to the linearized theory of a planar system (§ 12.6), the boundary conditions on the airfoil may be applied to its projection on the x axis instead of to the airfoil itself. Hence, the conditions 7 and 8 of § 13.2 should be satisfied on the segment (—1,1) of the x axis. On the corresponding £ plane, these conditions are to be satisfied on the unit circle.

The complex acceleration function is transformed as

dw dw dt, dw dw dz

Tz^llJz dt^dzTt ( ‘

* The symbol і comes from the complex representalion of harmonic oscillation. It is entirely different from the symbol j in Eq. 6. The functions <j>(x, y), u(x, y) do not involve j, but they may involve i. The symbol j is used to separate the potential and stream functions, but і is used to denote a change of phase angle in time, (/ ф — I.

dz Ж
The function	is the scale factor of the transformation.	Physically it
is the ratio of the length of an acceleration vector on the z plane to that of the transformed vector on the £ plane. Now on the airfoil (the unit circle on the £ plane),
sin 0|
(3)

Therefore, if the vertical component of the acceleration on the airfoil in

Fig. 13.2. Conformal mapping of a line segment into a circle.

z plane is a’v(x, 0, t), the component of acceleration normal to the unit circle in the £ plane must be

a’n(r =1,0 = cos-1 x, t) = a y(x, 0, t) sin 0 (4)

This correspondence must be remembered in imposing boundary condi­tions on the £ plane.

The condition at infinity on the z plane is that the acceleration potential ф tends to a constant when z -> oo. Since the limit of dz/d£ as z tends to infinity is finite (= 1/2), the condition at infinity on the £ plane is

lim Rl (w) — const

RH-ю

Our problem is then to find a complex acceleration potential which satisfies Eqs. 4 and 5 above, Eq. 7 of § 13.2, and the Kutta-Joukowski condition.

According to Eq. 5, the function w can be posed in the form of a Laurent series

w(£) = + yf + • • • (6)

where the constant term has been put to zero, because it contributes nothing to the acceleration field. The coefficients Аг, Л2, • • • can be determined according to the boundary condition 4 on the unit circle £ = eje. The Kutta-Joukowski condition is satisfied if series 6 converges at the point £ = 1 corresponding to the trailing edge.

It remains to satisfy the velocity boundary condition 7 of § 13.2, the velocity being given by Eq. 12 of that section. It will generally be found, however, that this boundary condition cannot be satisfied by the function w(0 in the form of Eq. 6 with the A’s chosen according to Eq. 4. To satisfy the additional condition it is expedient to add to series 6 a term that contributes nothing to the normal acceleration on the unit circle, but yet does contribute to the normal velocity on the airfoil. Such a term can be readily found. It can be shown that a source-sink doublet, with an axis tangent to a circle, will have that circle as one of its streamlines. Hence a doublet (in acceleration potential), with axis tangent to a unit circle, produces zero acceleration normal to that circle. If such a doublet lies at the leading edge of the airfoil, its complex potential is

where A0 is an arbitrary real constant. Such a term makes the leading edge of the airfoil a singular point, where the pressure tends to infinity like R-1!*, R being the distance from the leading edge. A singularity at the leading edge of this nature is found in the thin-airfoil theory in the subsonic steady-state case. Hence, its presence in the unsteady subsonic case is to be expected. With Eq. 1, we have

w(0 – + – f + + ‘

No other singular point is permitted on the airfoil. Hence the series 8 must converge everywhere on the unit circle, except at the leading edge, where it diverges logarithmically. It will be shown that by assuming the form 8 all the boundary conditions can be satisfied. That the solution so obtained is the unique solution can be proved.