Trefftz-plane force calculation

As discussed in Section 6.4.4, the Trefftz-plane provides an alternative to the near-field result (6.6) for calculating the wind-axes forces. A suitable discrete formulation of the Trefftz-plane integrals which is applicable to the VL method here was already given in Section 5.8.2. To apply those results it is first necessary to define the piecewise-constant wake potential jump distribution д^>г for each h. v. “chord strip," shown in Figure 6.6, whose h. v.’s have their trailing legs superimposed in the Trefftz-plane.

Дфг = Г (6.51)

strip

The summation is only over the h. v.’s within that chord strip, indicated in Figure 6.6. The normalized version of expression (5.81) for the wake-normal velocity дф/диг and expressions (5.77), (5.78), (5.82) for the forces Y, L, D-і can then be used as written.

6.5.7 Stability and control derivative calculation

The VL method is well suited to rapid calculation of stability and control derivatives in the small-angle operating range a, P, p,q, r^ 1. The calculation can be performed by finite-differencing slightly perturbed flow solutions, e. g.

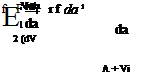A more economical alternative is to implicitly differentiate the overall force and moment summations with respect to each parameter via the chain rule, noting that rj as given by (6.41) and Vi as given by (6.42) have relatively simple dependencies on the parameters. For example, the a-derivatives of the following quantities can be evaluated in parallel with each quantity itself.

Note how each derivative calculation uses the derivatives calculated earlier. The final result (6.58) is the sought-after force stability derivatives with respect to a. The same procedure is used for the moment deriva­tive vector. The procedure is also repeated for all the remaining parameters e, p,q, r, St. The advantage of this direct differentiation method over the finite-difference approach (6.52) is that it is economical and effectively exact.