2-D Inviscid, Linearized, Thin Airfoil Theories

15.7.1.1 Incompressible Flow (Mo = 0)

Cambered Plate Geometry

Given the thin cambered plate equation

one calculates d'(x) to be

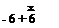
d'(x) = A 1

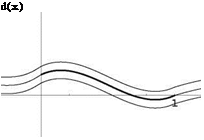
Fig. 15.25 Thin cambered d(x)

plate

Fourier Coefficients

The Fourier coefficients A0, A1, A2,…, An for this thin cambered plate are obtained from the equation

d'[x(t)] – a = — A0 + ^ An cos nt

n=1

Changing variable from x to t in d'(x) yields

d'[x(t)] = A ^ 1 — 3(1 — cos t) + 3(1 — cos t)2^

/ 1 3 2 A

= A — 2 + 2 cos21 = — (1 + 3cos2t)

where we have made use of the identity cos21 = (1 + cos 2t )/2. Substitution in the above equation provides by simple identification all the Fourier coefficients

A3

Ao = a — , A1 = 0, A2 = A, A3 = ••• = An = 0, n > 3

From the result for A0 one finds aadapt = A.

Sketch of the flow at the incidence of adaptation is in Fig. 15.26.

Definition of Aerodynamic Center

The aerodynamic center is the point about which the moment of the aerodynamic forces is independent of incidence.

Fig. 15.26 Thin cambered plate at incidence of adaptation and some streamlines

Aerodynamic Coefficients

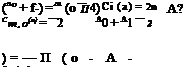The aerodynamic coefficients C;(a), Cm, o(a) and Cm, a.c. are all expressed in terms of the Fourier coefficients, i. e.

n 3n

Cm, a.c. = ~~r (A1 — A2) = A

4 16

Static Equilibrium About an Axis

The change of moment formula gives the aerodynamic moment coefficient at the mid-chord, x = 2

n 5 A 1 A n A

a — + 2n a — = a +

2 8 2 4 2 8

The equilibrium angle aeq is such that Cm 1 (aeq) = 0. Hence

A

aeq = —8