2-D Inviscid, Linearized, Thin Airfoil Theories

15.8.1.1 Incompressible Flow (Mo = 0)

Profile Geometry

Consider a half-double wedge profile of chord c of equation

f + (x) = d(x) + 1 e(x) = 0x, 0 < x < §
f + (x) = d(x) + §e(x) = 0(c – x), § < x < c

1

f (x) = d(x) – §e(x) = 0, 0 < x < c
See Fig. 15.30. The camber d(x) and thickness e(x) distributions are given by

d(x) = 1 (f+(x) + f-(x) = §0x, 0 < x < §
d(x) = 1 (f + (x) + f-(x) = 10(c – x), § < x < c

e(x) = f+(x) — f-(x) = 0x, 0 < x < §
e(x) = f +(x) — f-(x) = 0(c — x), § < x < c

Fourier Coefficients

The expressions of the Fourier coefficients A0 and An in the expansion of the vorticity for an arbitrary profile are

z/c

в/2

0.5

Fig. 15.30 Half double-wedge geometry

1 п. 2 n.

A0 = a — d [x(t)]dt, An — d [x(t)]cosntdt

п о п о

A0 and A2 is given by

Ao — a — — dt + ^ ^—— ) dt[ — a

A1 is given by

22 0 п 0 2 0 2 A1 — costdt + — costdt — {1 — (—1)} — 0

п 02 п 2 п 2 п

A2 is given by

2 2 0 п 0 2 0 A2 — – — cos2tdt + — — cos2tdt — — — {0 — (—0)} — 0

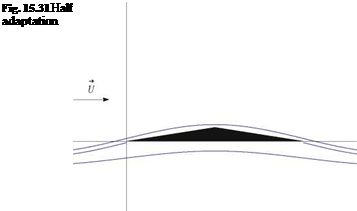
The incidence of adaptation aadapt is such that A0 — 0. Here we have aadapt — 0. See Fig. 15.31.

Definition of Aerodynamic Center

The aerodynamic center is the point about which the moment of the aerodynamic forces is independent of a.

Aerodynamic Coefficients

The aerodynamic coefficients C;(a) and Cm, o(a) are given in terms of the Fourier coefficients

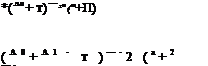Cl (a)

Cm, o(a) —