A GENERALIZED CONDITION OF OSCILLATION

Nonlinearity Ф is replaced in Figure 12.3 by its SIDF N(X, u). It is then straightforward to transform Figure 12.3 into Figure 12.4.a, with Ді replaced by N(X, w). Assume a fixed value for matrix Д2 (and thus for the associated vector <5 of parametric uncertainties) in Figure 12.3.

In the case of a SISO nonlinearity Ф, the necessary condition for the existence of a limit-cycle is:

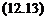l-Fi(P(ju>),A2)N(X, u) =0

In the general case of a MIMO nonlinearity, the necessary condition becomes (Gray and Nakhla, 1981):

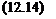det(I – Fl(P(juJ),A2)N(X, u)) = 0

X and to are fixed in this subsection, so that N(X, ш) is a constant mat­rix. As a consequence, the matrix Fu(P(jw),N(X, u))) (i. e. the transfer matrix at frequency o>, seen by the real model perturbation Д 2 in figure 12.4.a) can be computed a priori.

Proposition 3..3 introduces a method for computing the robustness margin r{X, ut), which measures the size of the smallest parametric un­certainty Д2, for which the necessary condition of oscillation in equation (12.14) is satisfied. Remember as a preliminary that r(X, u>) is a robust­ness margin, while the s. s.v. is homogeneous to the inverse of a robustness margin.

Definition 3..2

г(Х, ш) = min(k І ЗД2 Є kD2 s. t. det(I – Fi(P{ju), A2)N(X, u)) = 0) (12.15)

with r(X, u>) = 0 if the nominal closed loop (obtained with Д2 = 0J satisfies equation (12.14). Conversely, r(X, ut) = 00 if no Д2 satisfies equation (12.14).

1 /l*A3(P22(M) )N(X, u;))f 0

PROPOSITION 3..3 If: 1/ r(X, w]

2/ d, et(I – then r(X, u) – 1 /fiA2(Fu(P(ju),N(X, u)))

Proof: Lemma 3..1 is used. let к = r(X, w) and Ді = N(X, ui). Using the first assumption of the Proposition, it can be claimed that:

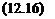det(I — P22{juj)A2) ф 0 УД2 Є kD2

Using then the second assumption, it is easy to see that the assumptions of Lemma 3..1 are satisfied, so that:

det(I-F,(P(jw),A2)t1)fO <t=> det(I-Fu(P(jw),Ai)A2)f0 (12.17) r(X, uj) thus coincides with l//iA2(Fu(P(ja>),lV(.X’, w))).

Remark: the second assumption in Proposition 3..3 means that the

necessary condition of oscillation is not satisfied at (X, ш) for the nom­inal closed loop system, since Fi ( P(Д) , Д2 ) = Pi p (Д ) when Д2 = 0.

Concerning the first assumption in Proposition 3..3, it is worth point­ing out that /ід2(Р22(Д)) measures the robust stability property of the transfer matrix Fi(P(s),A2) [13] (i. e. the transfer matrix between u andy in Figure 12.3). Assume indeed that P(s) is asymptotically stable. Define then the stability margin kmax as the maximal value of k, such that the transfer matrix Fi(P(s),A2) is asymptotically stable for all Д2 Є kD2. kmax can be computed as:

77— = max HA2(P22(j<j)) (12.18)

Kmax

As a final point, the following Corollary proposes to compute a lower bound of the robustness margin r(X, u>) when the first assumption in Proposition 3..3 is not satisfied.

Corollary 3..4 If – et( i – Pi—( x( x,-) ) – о, then:

r(x’“) – <іг’19> Proof:

• If/iAJ(i;,u(P(jci;))7V(-X’,w))) > мд2(Р22(7^)), the assumptions ofPro – position 3..3 are satisfied and the above Corollary reduces to this Pro­position (Inequation (12.19) becomes an equality).

• IfHA2(Fu(P(ju),N(X, u))) < fJ. A2(P22(jw)), let к < 1 /HA2(P22(ju)) and F( p F( F, f(. By definition of /гд2(Р22(.?А;)):

det(I – P22(ju)A2) ф 0 УД2 Є kD2 (12.20)

Using then the assumption of the Corollary, it is straightforward to see that the assumptions of Lemma 3..1 are here again satisfied, so that:

det{I-F,(PUu),A2)Ai)*0 <=► det(I-Fu(PU^),Al)A2)^0 (12.21)

Noting then that к < l/i/,A2(Pu(P(ju),N(X, w))), it can be claimed that:

det(I – Fu(P(ju), Ді)Д2) Ф 0 УД2 Є kD2

As a consequence:

det(I – Ft(P{jш),А2)Аі) ф 0 УД2 Є kD2

The necessary condition of oscillation of equation (12.14) is not satisfied, and к is consequently a lower bound of the robustness margin r(X, w).