Aileron-Reversal Theories
Aileron reversal is closely related to wing torsional divergence, involving also quasi-static wing twist. Aileron reversal limits roll maneuverability at high airspeeds and low altitude. At airspeeds where wings are still within structural limits, torques exerted on wings by deflected ailerons can twist the wing in the opposite direction enough to cancel much of the aileron’s lift or rolling moment, and even to reverse the aileron’s effect. The airspeed at which complete rolling moment cancellation occurs is called the aileron-reversal speed (Figure 19.2). Like a wing’s flutter or torsional divergence speeds, aileron-reversal speed should be only a theoretical number, quite outside of the airplane’s operating envelope and with an adequate safety margin.
|
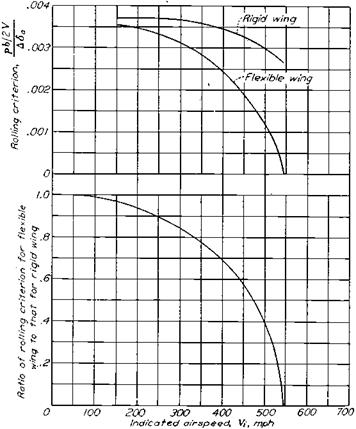
Figure 19.2 An example of the effect of wing flexibility on available rolling velocity. Data for the Republic P-47C-1-RE at an altitude of 4,000 feet. Aileron reversal occurs at 545 miles perhour. (From Toll, NACA Rept. 868, 1947) |
Theoretical work on aileron reversal fits into Etkin’s quasi-static category. The earliest published work on aileron reversal was necessarily simplified, with the computing resources available at that time (Cox and Pugsley, 1932). The wing is represented in the same semirigid manner described for the wing torsional divergence problem. That is, a reference section along the wing is selected and the elastic restoring moment is related to the angular deflection at that station. A modern example of the semi-rigid approach to aileron reversal is given by Bisplinghoff and Ashley (1962).
An extension of the semi-rigid approach yields one of the most useful concepts in static aeroelasticity, the ratio of elastic to rigid control surface effectiveness. For the simple two-dimensional case, this ratio depends only on the flexibility influence coefficient, or twist angle per unit applied torque, the changes in section lift coefficient per unit section angle of attack and aileron deflection, the change in section moment coefficient about the aerodynamic center with aileron deflection, and the ratio of the distance between the elastic axis and aerodynamic center to the section chord length.
In a sense, everything that came after the two-dimensional, or semi-rigid, approach was refinement, to deal adequately with problems of real airplanes. For example, in 1945, Dr. Alexander H. Flax expressed the wing twist spanwise distribution as a superposition of modes with undetermined magnitudes. Mode magnitudes are found by the virtual work principle, in a solution of simultaneous algebraic equations. Many authors call this Galerkin’s method. Still later, finite-element methods permitted a direct solution that eliminated the need for assumed mode shapes.