Airfoil Characteristics
Before discussing the theoretical calculation of airfoil properties, let us examine some typical results. During the 1930s and 1940s, the NACA carried out numerous measurements of the lift, drag, and moment coefficients on the standard NACA airfoils. These experiments were performed at low speeds in a wind tunnel where the constant-chord wing spanned the entire test section from one sidewall to the other. In this fashion, the flow “sees” a wing without wing tips—a so-called infinite wing,
which theoretically stretches to infinity along the span (in the у direction in Figure 4.1). Because the airfoil section is the same at any spanwise location along the infinite wing, the properties of the airfoil and the infinite wing are identical. Hence, airfoil data are frequently called infinite wing data. (In contrast, we see in Chapter 5 that the properties of a finite wing are somewhat different from its airfoil properties.)
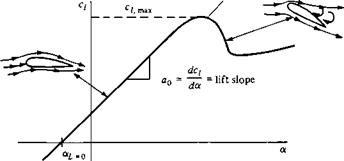
The typical variation of lift coefficient with angle of attack for an airfoil is sketched in Figure 4.4. At low-to-moderate angles of attack, с/ varies linearly with a; the slope of this straight line is denoted by ao and is called the lift slope. In this region, the flow moves smoothly over the airfoil and is attached over most of the surface, as shown in the streamline picture at the left of Figure 4.4. However, as a becomes large, the flow tends to separate from the top surface of the airfoil, creating a large wake of relatively “dead air” behind the airfoil as shown at the right of Figure 4.4. Inside this separated region, the flow is recirculating, and part of the flow is actually moving in a direction opposite to the freestream—so-called reversed flow. (Refer also to Figure 1.36.) This separated flow is due to viscous effects and is discussed in Chapter 15. The consequence of this separated flow at high a is a precipitous decrease in lift and a large increase in drag; under such conditions the airfoil is said to be stalled. The maximum value of С/, which occurs just prior to the stall, is denoted by ci, max; it is one of the most important aspects of airfoil performance, because it determines the stalling speed of an airplane. The higher is c/>max, the lower is the stalling speed. A great deal of modem airfoil research has been directed toward increasing c/,max. Again examining Figure 4.4, we see that c; increases linearly with а until flow separation begins to have an effect. Then the curve becomes nonlinear, q reaches a maximum value, and finally the airfoil stalls. At the other extreme of the curve, noting Figure 4.4, the lift at a = 0 is finite; indeed, the lift goes to zero only when the airfoil is pitched to some negative angle of attack. The value of a when lift equals zero is called the zero-lift angle of attack and is denoted by chl=o- For a
|
symmetric airfoil, aL=0 — 0, whereas for all airfoils with positive camber (camber above the chord line), aL=0 is a negative value, usually on the order of —2 or —3°.
The inviscid flow airfoil theory discussed in this chapter allows us to predict the lift slope ao and aL=0 for a given airfoil. It does not allow us to calculate c/.max, which is a difficult viscous flow problem, to be discussed in Chapters 15 to 20.
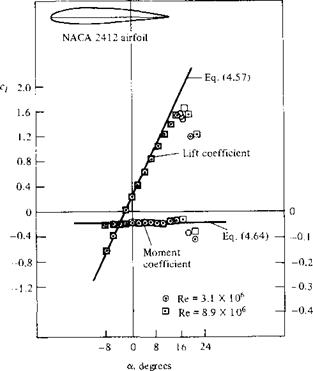
Experimental results for lift and moment coefficients for the NACA 2412 airfoil are given in Figure 4.5. Here, the moment coefficient is taken about the quarter-chord point. Recall from Section 1.6 that the force-and-moment system on an airfoil can be transferred to any convenient point; however, the quarter-chord point is commonly used. (Refresh your mind on this concept by reviewing Section 1.6, especially Figure 1.19.) Also shown in Figure 4.5 are theoretical results to be discussed later. Note that the experimental data are given for two different Reynolds numbers. The lift slope ao is not influenced by Re; however, c/,max is dependent upon Re. This makes sense, because c/,max is governed by viscous effects, and Re is a similarity parameter that governs the strength of inertia forces relative to viscous forces in the flow. [See
|
Figure 4.5 Experimental data for lift coefficient and moment coefficient about the quarter-chord point for an NACA 2412 airfoil. (Source: Data obtained from Abbott and von Doenhoff, Reference 1 1.) Also shown is a comparison with theory described in Section 4.8. |
Section 1.7 and Equation (1.35).] The moment coefficient is also insensitive to Re except at large a. The NACA 2412 airfoil is a commonly used airfoil, and the results given in Figure 4.5 are quite typical of airfoil characteristics. For example, note from Figure 4.5 that (Xl=о = —2.1°, c/ max ~ 1 -6, and the stall occurs at a ~ 16°.
This chapter deals with airfoil theory for an inviscid, incompressible flow; such theory is incapable of predicting airfoil drag, as noted earlier. However, for the sake of completeness, experimental data for the drag coefficient cd for the NACA 2412 airfoil are given in Figure 4.6 as a function of the angle of attack.[14] The physical source of this drag coefficient is both skin friction drag and pressure drag due to flow separation (so-called form drag). The sum of these two effects yields the profile drag coefficient cd for the airfoil, which is plotted in Figure 4.6. Note that cd is sensitive to Re, which is to be expected since both skin friction and flow separation are viscous effects. Again, we must wait until Chapters 15 to 20 to obtain some tools for theoretically predicting cd.