. Applied Aerodynamics: The Delta Wing

In Part 3 of this book, we will see that supersonic flow is dramatically different from subsonic flow in virtually all respects—the mathematics and physics of these two flow regimes are totally different. Such differences impact the design philosophy of aircraft for supersonic flight in comparison to aircraft for subsonic flight. In particular, supersonic airplanes usually have highly swept wings (the reasons for this are discussed in Part 3). A special case of swept wings is those aircraft with a triangular planform—called delta wings. A comparison of the planform of a conventional swept wing was shown in Figure 5.30. Two classic examples of aircraft with delta wings are the Convair F-102A, the first operational jet airplane in the United States to be designed with a delta wing, shown in Figure 5.37a, and the space shuttle, basically a hypersonic airplane, shown in Figure 5.31b. In reality, the planform of the space shuttle is more correctly denoted as a double-delta shape. Indeed, there are several variants of the basic delta wing used on modem aircraft; these are shown in Figure 5.38. Delta wings are used on many different types of high-speed airplanes around the world; hence, the delta planform is an important aerodynamic configuration.

Ui) Figure 5.37 Some delta-winged vehicles, (a) The Convair F-l 02A. (Courtesy of the U. S. Air Force.}

Question: Since delta-winged aircraft are high-speed vehicles, why are we dis­cussing this topic in the present chapter, which deals with the low-speed, incompress­ible flow over finite wings? The obvious answer is that all high-speed aircraft fly at low speeds for takeoff and landing; moreover, in most cases, these aircraft spend the

Figure 5.37 (continued) Some delta-winged vehicles, (b) The space shuttle. (Courtesy of NASA.)

Figure 5.38 Four versions of a delta-wing planform.

(From Loftin, Reference 48.)

vast majority of their flight time at subsonic speeds, using their supersonic capability for short “supersonic dashes,” depending on their mission. Several exceptions are, of course, the Concorde supersonic transport which cruises at supersonic speeds across oceans, and the space shuttle, which is hypersonic for most of its reentry into the earth’s atmosphere. However, the vast majority of delta-winged aircraft spend a great deal of their flight time at subsonic speeds. For this reason, the low-speed aerodynamic characteristics of delta wings are of great importance; this is accentuated by the rather different and unique aerodynamic aspects associated with such delta wings. Therefore, the low-speed aerodynamics of delta wings has been a subject of much serious study over the past years, going back as far as the early work on delta wings by Alexander Lippisch in Germany during the 1930s. This is the answer to our question posed above—in the context of our discussion on finite wings, we must give the delta wing some special attention.

The subsonic flow pattern over the top of a delta wing at angle of attack is sketched in Figure 5.39. The dominant aspect of this flow are the two vortex patterns that occur in the vicinity of the highly swept leading edges. These vortex patterns are created by the following mechanism. The pressure on the bottom surface of the wing at the angle of attack is higher than the pressure on the top surface. Thus, the flow on the bottom surface in the vicinity of the leading edge tries to curl around the leading edge from the bottom to the top. If the leading edge is sharp, the flow will

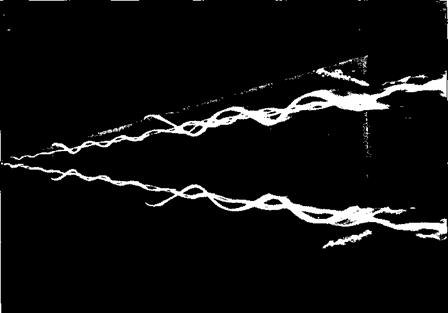
separate along its entire length. (We have already mentioned several times that when low-speed, subsonic flow passes over a sharp convex comer, inviscid flow theory predicts an infinite velocity at the corner, and that nature copes with this situation by having the flow separate at the corner. The leading edge of a delta wing is such a case.) This separated flow curls into a primary vortex which exists above the wing just inboard of each leading edge, as sketched in Figure 5.39. The stream surface which has separated at the leading edge (the primary separation line Л) in Figure 5.39) loops above the wing and then reattaches along the primary attachment line (line A in Figure 5.39). The primary vortex is contained within this loop. A secondary vortex is formed underneath the primary vortex, with its own separation line, denoted by S2 in Figure 5.39, and its own reattachment line A%. Notice that the surface streamlines flow away from the attachment lines A and Аг on both sides of these lines, whereas the surface streamlines tend to flow toward the separation fines S) and Sj and then simply lift off the surface along these lines. Inboard of the leading-edge vortices, the surface streamlines are attached, and flow downstream virtually is undisturbed along a series of straight-line rays emanating from the vertex of the triangular shape. A graphic illustration of the leading-edge vortices is shown in both Figures 5.40 and 5.41. In Figure 5.40, we see a highly swept delta wing mounted in a water tunnel. Filaments of colored dye are introduced at two locations along each leading edge. This photograph, taken from an angle looking down on the top of the wing, clearly shows the entrainment of the colored dye in the vortices. Figure 5.41 is a photograph of the vortex pattern in the crossflow plane (the crossflow plane is shown in Figure 5.39). From the photographs in Figures 5.40 and 5.41, we clearly see that the leading-

Figure 5.40 Leading-edge vortices over the top surface of a delta wing at angle of attack. The vortices are made visible by dye streaks in water flow. (Courtesy of H. Werle, ONERA, France. Also in Van Dyke, Milton, An Album of Fluid Motion, The Parabolic Press, Stanford, CA, 1982.)

edge vortex is real and is positioned above and somewhat inboard of the leading edge itself.

The leading-edge vortices are strong and stable. Being a source of high energy, relatively high-vorticity flow, the local static pressure in the vicinity of the vortices is small. Hence, the surface pressure on the top surface of the delta wing is reduced near the leading edge and is higher and reasonably constant over the middle of the wing. The qualitative variation of the pressure coefficient in the spanwise direction (the у direction as shown in Figure 5.39) is sketched in Figure 5.42. The spanwise variation of pressure over the bottom surface is essentially constant and higher than the freestream pressure (a positive Cp). Over the top surface, the spanwise variation in the midsection of the wing is essentially constant and lower than the freestream pressure (a negative Cp). However, near the leading edges the static pressure drops considerably (the values of Cp become more negative). The leading-edge vortices are literally creating a strong “suction” on the top surface near the leading edges. In Figure 5.42, vertical arrows are shown to indicate further the effect on the spanwise lift distribution; the upward direction of these arrows as well as their relative length show the local contribution of each section of the wing to the normal force distribution. The suction effect of the leading-edge vortices is clearly shown by these arrows.

The suction effect of the leading-edge vortices enhances the lift; for this reason, the lift coefficient curve for a delta wing exhibits an increase in С/ for values of a at

Figure 5.41 The flow field in the crossflow plane above a delta wing at angle of attack, showing the two primary leading-edge vortices. The vortices are made visible by small air bubbles in water. (Courtesy of H. Werle, ONERA, France. Also in Van Dyke, Milton, An Album of Fluid Motion, The Parabolic Press, Stanford, CA, 1982.)

Figure 5.42 Schematic of the spanwise pressure coefficient distribution across a delta wing. (Courtesy of John Stollery, Cranfield Institute of Technology, England. j

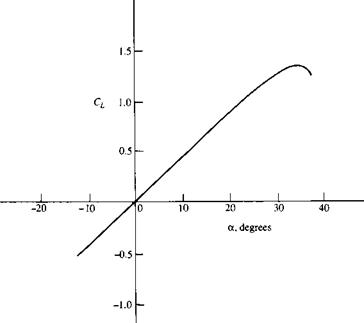
which conventional wing planforms would be stalled. A typical variation of С/ with a for a 60° delta wing is shown in Figure 5.43. Note the following characteristics:

1. The lift slope is small, on the order of 0.05/degree.

2. However, the lift continues to increase to large values of a; in Figure 5.43, the stalling angle of attack is on the order of 35°. The net result is a reasonable value of ax, on the order of 1.3.

The next time you have an opportunity to watch a delta-winged airplane take off or land, say, for example, the televised landing of the space shuttle, note the large angle of attack of the vehicle. Moreover, you will understand why the angle of attack is large—because the lift slope is small, and hence the angle of attack must be large enough to generate the high values of Cl required for low-speed flight.

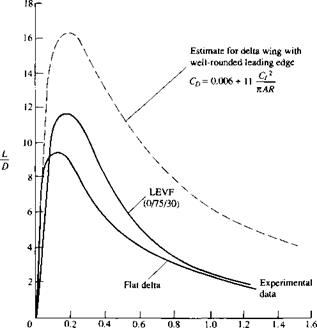
The suction effect of the leading-edge vortices, in acting to increase the normal force, consequently, increases the drag at the same time it increases the lift. Hence, the aerodynamic effect of these vortices is not necessarily advantageous. In fact, the lift-to-drag ratio L/D for a delta planform is not so high as conventional wings. The typical variation of L/D with Cl for a delta wing is shown in Figure 5.44; the results for the sharp leading edge, 60° delta wing are given by the lower curve. Note that the maximum value of L/D for this case is about 9.3—not a particularly exciting value for a low-speed aircraft.

Figure 5.43 Variation of lift coefficient for a flat delta wing with angle of attack. (Courtesy of John Stollery, Cranfield Institute of Technology England.)

CL Figure 5.44 The effect of leading-edge shape on the lift-to-drag ratio for a delta wing of aspect ratio 2.31. The two solid curves apply to a sharp leading edge, and the dashed curve applies to a rounded leading edge. LEVF denotes a wing with a leading-edge vortex flap. (Courtesy of John Stollery, Cranfield Institute of Technology, England.)

There are two other phenomena that are reflected by the data in Figure 5.44. The first is the effect of greatly rounding the leading edges of the delta wing. In our previous discussions, we have treated the case of a sharp leading edge; such sharp edges cause the flow to separate at the leading edge, forming the leading-edge vortices. On the other hand, if the leading-edge radius is large, the flow separation will be minimized, or possibly will not occur. In turn, the drag penalty discussed above will not be present, and hence the L/D ratio will increase. The dashed curve in Figure 5.44 is the case for a 60° delta wing with well-rounded leading edges. Note that (L/D)mm for this case is about 16.5, almost a factor of 2 higher than the sharp leading-edge case. However, keep in mind that these are results for subsonic speeds. There is a major design compromise reflected in these results. At the beginning of this section, we mentioned that the delta-wing planform with sharp leading edges is advantageous for supersonic flight—its highly swept shape in combination with sharp leading edges has a low supersonic drag. However, at supersonic speeds this advantage will be negated if the leading edges are rounded to any great extent. We will find in our study of supersonic flow in Part 3 that a blunt-nosed body creates very large values of wave drag. Therefore, leading edges with large radii are not appropriate for supersonic aircraft; indeed, it is desirable to have as sharp a leading edge as is practically possible for supersonic airplanes. A singular exception is the design of the space shuttle. The leading-edge radius of the space shuttle is large; this is due to three features that combine to make such blunt leading edges advantageous for the shuttle. First, the shuttle must slow down early during reentry into the earth’s atmosphere to avoid massive aerodynamic heating (aspects of aerodynamic heating are discussed in Part 4). Therefore, in order to obtain this deceleration, a high drag is desirable for the space shuttle; indeed, the maximum L/D ratio of the space shuttle during reentry is about 2. A large leading-edge radius, with its attendant high drag, is therefore advantageous. Second, as we will see in Part 4, the rate of aerodynamic heating to the leading edge itself—a region of high heating—is inversely proportional to the square root of the leading-edge radius. Hence, the larger the radius, the smaller will be the heating rate to the leading edge. Third, as already explained above, a highly rounded leading edge is certainly advantageous to the shuttle’s subsonic aerodynamic characteristics. Hence, a well-rounded leading edge is an important design feature for the space shuttle on all accounts. However, we must be reminded that this is not the case for more conventional supersonic aircraft, which demand very sharp leading edges. For these aircraft, a delta wing with a sharp leading edge has relatively poor subsonic performance.

This leads to the second of the phenomena reflected in Figure 5.44. The middle curve in Figure 5.44 is labeled LEVF, which denotes the case for a leading-edge vortex flap. This pertains to a mechanical configuration where the leading edges can be deflected downward through a variable angle, analogous to the deflection of a conventional trailing-edge flap. The spanwise pressure-coefficient distribution for this case is sketched in Figure 5.45; note that the direction of the suction due to the

Figure 5.45 A schematic of the spanwise pressure coefficient distribution over the top of a delta wing as modified by leading-edge vortex flaps. (Courtesy of John Stollery, Cranfield Institute of Technology, England.!

leading-edge vortice is now modified in comparison to the case with no leading-edge flap shown earlier in Figure 5.42. Also, returning to Figure 5.39, you can visualize what the wing geometry would look like with the leading edge drooped down; a front view of the downward deflected flap would actually show some projected frontal area. Since the pressure is low over this frontal area, the net drag can decrease. This phenomenon is illustrated by the middle curve in Figure 5.44, which shows a generally higher L/D for the leading-edge vortex flap in comparison to the case with no flap (the flat delta wing).

In summary, the delta wing is a common planform for supersonic aircraft. In this section, we have examined the low-speed aerodynamic characteristics of such wings and have found that these characteristics are in some ways quite different from a conventional planform.