Applied Aerodynamics: The Flow Over a Sphere—The Real Case

The present section is a complement to Section 3.18, in which the real flow over a cir­cular cylinder was discussed. Since the present chapter deals with three-dimensional flows, it is fitting at this stage to discuss the three-dimensional analog of the circular cylinder, namely, the sphere. The qualitative features of the real flow over a sphere are similar to those discussed for a cylinder in Section 3.18—the phenomenon of flow separation, the variation of drag coefficient with a Reynolds number, the precip­itous drop in drag coefficient when the flow transits from laminar to turbulent ahead of the separation point at the critical Reynolds number, and the general structure of the wake. These items are similar for both cases. However, because of the three­dimensional relieving effect, the flow over a sphere is quantitatively different from that for a cylinder. These differences are the subject of the present section.

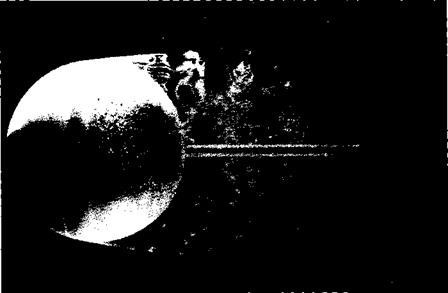
The laminar flow over a sphere is shown in Figure 6.9. Here, the Reynolds number is 15,000, certainly low enough to maintain laminar flow over the spherical

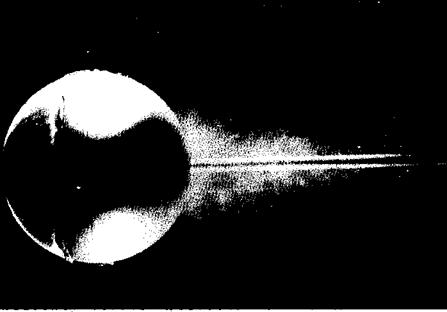
surface. However, in response to the adverse pressure gradient on the back surface of the sphere predicted by inviscid, incompressible flow theory (see Section 6.4 and Figure 6.6), the laminar flow readily separates from the surface. Indeed, in Figure 6.9, separation is clearly seen on the. forward surface, slightly ahead of the vertical equator of the sphere. Thus, a large, fat wake trails downstream of the sphere, with a consequent large pressure drag on the body (analogous to that discussed in Section 3.18 for a cylinder.) In contrast, the turbulent flow case is shown in Figure 6.10. Here, the Reynolds number is 30,000, still a low number normally conducive to laminar flow. However, in this case, turbulent flow is induced artificially by the presence of a wire loop in a vertical plane on the forward face. (Trip wires are frequently used in experimental aerodynamics to induce transition to turbulent flow; this is in order to study such turbulent flows under conditions where they would not naturally exist.) Because the flow is turbulent, separation takes place much farther over the back surface, resulting in a thinner wake, as can be seen by comparing Figures 6.9 and 6.10. Consequently, the pressure drag is less for the turbulent case.

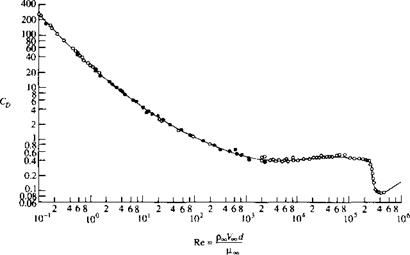
The variation of drag coefficient Co with the Reynolds number for a sphere, is shown in Figure 6.11. Compare this figure with Figure 3.39 for a circular cylinder;

the С о variations are qualitatively similar, both with a precipitous decrease in Cp near a critical Reynolds number of 300,000, coinciding with natural transition from laminar to turbulent flow. However, quantitatively the two curves are quite different. In the Reynolds number range most appropriate to practical problems, that is, for Re > 1000, the values of CD for the sphere are considerably smaller than those for a cylinder—a classic example of the three-dimensional relieving effect. Reflecting on Figure 3.39 for the cylinder, note that the value of CD for Re slightly less than the critical value is about 1 and drops to 0.3 for Re slightly above the critical value. In contrast, for the sphere as shown in Figure 6.11, Cp is about 0.4 in the Reynolds number range below the critical value and drops to about 0.1 for Reynolds numbers above the critical value. These variations in Co for both the cylinder and sphere are classic results in aerodynamics; you should keep the actual Co values in mind for future reference and comparisons.

As a final point in regard to both Figures 3.39 and 6.11, the value of the critical Reynolds number at which transition to turbulent flow takes place upstream of the separation point is not a fixed, universal number. Quite the contrary, transition is influenced by many factors, as will be discussed in Part 4. Among these is the amount of turbulence in the freestream; the higher the freestream turbulence, the more readily transition takes place. In turn, the higher the freestream turbulence, the lower is the value of the critical Reynolds number. Because of this trend, calibrated spheres are used in wind-tunnel testing actually to assess the degree of freestream turbulence in the test section, simply by measuring the value of the critical Reynolds number on the sphere.