B. M. Jones’ wake traverse method for determining profile drag

In the wake close behind a body the static pressure, as well as the velocity, will vary from the value in the free stream outside the wake. B. Melville Jones allowed for this fact by assuming that, in any given stream tube between planes 1 (close to the body) and 2 (far downstream), the stagnation pressure could be considered to remain constant. This is very nearly the case in practice, even in turbulent wakes.

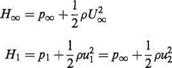Let Hx be the stagnation pressure in any stream tube at plane 0 and Hi = #2 be its value in the same stream tube at planes 1 and 2. Then

The velocities are given by

Substituting the values for Ux and м2 into Eqn (7.166) gives

D = lf л/Ні – px{^Hx -px – VНу – px)dy2 (7.167)

To refer this to plane 1, the equation of continuity in the stream tube must be used, i. e.

Ml буї = М2 6y2

or

(7.168)

Referred to the wake at plane 1, Eqn (7.167) then becomes

D = 2 f ^/Hi-pi(y/Hx-px – у/Hi – Poo) dyi (7.169)

In order to express Eqn (7.169) non-dimensionally, the profile-drag coefficient CDp is used. For unit span:

.P^OOC C(H°° Poo)

* A. Betz, ZFM, 16, 42, 1925.

+ B. Melville Jones, ARCR and M, 1688, 1936.

so that Eqn (7.169) becomes

It will be noticed again that this integral needs to be evaluated only across the wake, because beyond the wake boundary the stagnation pressure H becomes equal to Hx so that the second term in the bracket becomes unity and the integrand becomes zero.

Equation (7.170) may be conveniently used in the experimental determination of profile drag of a two-dimensional body when it is inconvenient, or impracticable, to use a wind-tunnel balance to obtain direct measurement. It can, in fact, be used to determine the drag of aircraft in free flight. All that is required is a traversing mechanism for a pitot-static tube, to enable the stagnation and static pressures H and p to be recorded at a series of positions across the wake, ensuring that measure­ments are taken as far as the undisturbed stream on either side, and preferably an additional measurement made of the dynamic pressure, Hx — px, in the incoming stream ahead of the body. In the absence of the latter it can be assumed, with reasonable accuracy, that Hx — px will be the same as the value of H — p outside the wake.

Using the recordings obtained from the traverse, values of H — p and H — px may be evaluated for a series of values of yi/c across the wake, and hence a corresponding series of values of the quantity

I Hi-pi Л ІНг-рЛ

у Нх px у у Hoc Poo J

By plotting a curve of this function against the variable yi/c a closed area will be obtained (because the integral becomes zero at each edge of the wake). The magni­tude of this area is the value of the integral, so that the coefficient CD? is given directly by twice the area under the curve.

In order to facilitate the actual experimental procedure, it is often more convenient to construct a comb or rake of pitot and static tubes, set up at suitable spacings. The comb is then positioned across the wake (it must be wide enough to read into the free stream on either side) and the pitot and static readings recorded.

The method can be extended to measure the drag of three-dimensional bodies, by making a series of traverses at suitable lateral (or spanwise) displacements. Each individual traverse gives the drag force per unit span, so that summation of these in a spanwise direction will give the total three-dimensional drag.