Bernoulli’s Equation

As will be portrayed in Section 3.19, the early part of the eighteenth century saw the flowering of theoretical fluid dynamics, paced by the work of Johann and Daniel Bernoulli and, in particular, by Leonhard Euler. It was at this time that the relation between pressure and velocity in an inviscid, incompressible flow was first understood.

The resulting equation is

Equation (3.12) is called Euler’s equation. It applies to an inviscid flow with no body forces, and it relates the change in velocity along a streamline d V to the change in pressure dp along the same streamline.

Equation (3.12) takes on a very special and important form for incompressible flow. In such a case, p — constant, and Equation (3.12) can be easily integrated between any two points 1 and 2 along a streamline. From Equation (3.12), with p = constant, we have

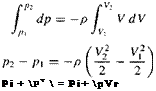or

[3.13]

Equation (3.13) is Bernoulli’s equation, which relates pi and Vt at point 1 on a streamline to pz and V2 at another point 2 on the same streamline. Equation (3.13)

can also be written as

In the derivation of Equations (3.13) and (3.14), no stipulation has been made as to whether the flow is rotational or irrotational—these equations hold along a streamline in either case. For a general, rotational flow, the value of the constant in Equation (3.14) will change from one streamline to the next. Flowever, if the flow is irrotational, then Bernoulli’s equation holds between any two points in the flow, not necessarily just on the same streamline. For an irrotational flow, the constant in Equation (3.14) is the same for all streamlines, and

The proof of this statement is given as Problem 3.1.

The physical significance of Bernoulli’s equation is obvious from Equations

(3.13) to (3.15); namely, when the velocity increases, the pressure decreases, and when the velocity decreases, the pressure increases.

Note that Bernoulli’s equation was derived from the momentum equation; hence, it is a statement of Newton’s second law for an inviscid, incompressible flow with no body forces. Flowever, note that the dimensions of Equations (3.13) to (3.15) are energy per unit volume (pV2 is the kinetic energy per unit volume). Flence, Bernoulli’s equation is also a relation for mechanical energy in an incompressible flow; it states that the work done on a fluid by pressure forces is equal to the change in kinetic energy of the flow. Indeed, Bernoulli’s equation can be derived from the general energy equation, such as Equation (2.114). This derivation is left to the reader. The fact that Bernoulli’s equation can be interpreted as either Newton’s second law or an energy equation simply illustrates that the energy equation is redundant for the analysis of inviscid, incompressible flow. For such flows, the continuity and momentum equations suffice. (You may wish to review the opening comments of Section 2.7 on this same subject.)

The strategy for solving most problems in inviscid, incompressible flow is as follows:

1. Obtain the velocity field from the governing equations. These equations, appro­priate for an inviscid, incompressible flow, are discussed in detail in Sections 3.6

and 3.7.

2. Once the velocity field is known, obtain the corresponding pressure field from Bernoulli’s equation.

However, before treating the general approach to the solution of such flows (Section 3.7), several applications of the continuity equation and Bernoulli’s equation are made to flows in ducts (Section 3.3) and to the measurement of airspeed using a Pitot tube (Section 3.4).

Example 3.1 I Consider an airfoil in a flow at standard sea level conditions with a freestream velocity of 50 m/s. At a given point on the airfoil, the pressure is 0.9 x 105 N/m2. Calculate the velocity at this point.

Solution

At standard sea level conditions, рх = 1.23 kg/m3 and px = 1.01 x 105 N/m2. Hence,

Pcо + pVl, = p + pV2

v – 01 x ‘O’ 7^1

U = 142.8 m/s