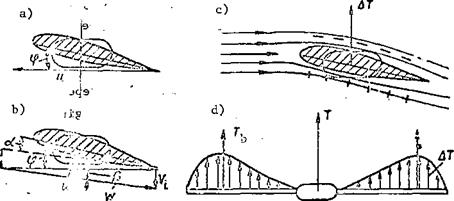
Blade Element Theory

In accordance with this theory, each element of the blade is considered as a small wing, which moves in a circular trajectory with speed u = 0)r (Figure 15a). If the profile of the blade were symmetrical and the incidence angle ф = 0, there would be no deflection of air downwards, and and T would be equivalent to zero.

For an asymmetrical profile and ф > 0, the airflow approaching the blade element is deflected downwards. This deflection, and as a consequence, the induced velocity will be larger, the larger the incidence angle of the element, and the greater the angular velocity or the rotation of the main rotor (Figure 15b).

Adding the vectors of circular and induced velocity, we obtain the result – /19 ing vector w = u +

The angle a between the chord of the blade element and the resultant velocity vector is termed the angle of attack of the blade element. The aerodynamic forces, arising from the main rotor blade, depend on this angle.

Examining the spectrum of the streamlines around a blade element, it can be observed that the streamlines have the same form as the spectrum of a wing (Figure 15c). On this basis we can state that the air pressure on the blade upper surface will be less than on the lower surface. Owing to the

24

Figure 15. Development of thrust force according to blade element theory

difference in pressure, there arises an element of thrust force AT (Figure 15c). If all the elements of force are summed, we obtain the thrust force of the entire rotor

T = Tg к

where к = number of blades

T – thrust of blade; T = EAT

в в

To determine the force of the main rotor, it is possible to utilize the formula for the lift force of a wing:

T=CTF-t-(o>R) (8)

where CT = thrust coefficient.

Because uiR = u (u is the circular velocity of the blade tip), it is pos­sible to write the formula for the thrust force in the following form:

T=CrFu?. (9)

The conclusion is that the thrust force of the main rotor is proportional to the thrust coefficient, the area swept out by the rotor, air density, and the square of the circular velocity of the blade tip.

For a given rotor at a constant air density, the thrust depends on the /20 number of revolutions and the thrust coefficient. The thrust coefficient depends on the pitch of the rotor (Figure 16).

The conclusions that have been outlined according to "impulsive theory" and "blade element theory" do not contradict each other, but are mutually supplementary. On the basis of these conclusions, it is possible to state that, in order to increase the thrust force of the main rotor, it is necessary to increase the pitch or the revolutions, or both of them at the same time.

Besides the thrust force, the rotation of the rotor gives rise to forces that resist rotation. We will consider these forces in the next section.