Boundary layer normal pressure (form) drag

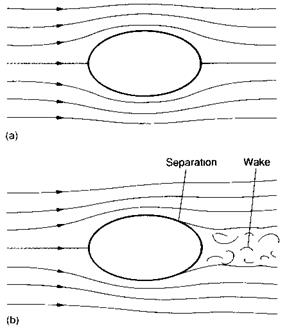
Without the influence of viscosity, the streamlines or stream surfaces would close up neatly behind all parts of the aircraft, and there would be no wake. For a symmetrical shape such as that shown in Fig. 4.1, the streamline pattern and the pressure distribution would also be symmetrical, as in Fig. 4.1(a), and therefore, there would be no net resultant force. In fact, theoretical analysis shows, that if there were no viscosity, the pressure distribution would result in no net drag force on any shape. In the real case shown in Fig. 4.1(b), and Fig. 4.2, the streamline pattern and pressure distribution are not symmetrical, and a wake of slow-moving air is formed at the rear.

On shapes such as that shown in Fig. 4.1, the air pressure reaches its min­imum value at about the position of maximum section depth. Thus, over the tail portion, the air is flowing from a low pressure to a high one. As we have previously stated, this condition is known as an adverse pressure gradient, since the flow is likely to separate. Even if the flow does not separate, an adverse pressure gradient promotes a rapid degradation of available energy in the boundary layer, resulting in a reduction in pressure over the rear. Thus, on average, there is a lower pressure on the rear of the section than on the front, and therefore, there is now a net drag force, which is known as the boundary layer normal pressure (form) drag.

When the flow does separate, as illustrated in Fig. 4.1(b), the pressure down­stream of the separation positions is nearly uniform at a low value. Hence, the boundary layer normal pressure (form) drag will be high.

In general, the further forward the separation positions are, the greater will be the area of low pressure, and the higher will be the drag.

Note, that since there is a loss of available energy in the boundary layer, Bernoulli’s relationship does not apply there, as it is based on the assumption that the amount of available energy remains constant. In the boundary layer and the wake, the speed and the pressure can be simultaneously lower than in the free-stream values.

The term boundary layer drag (profile drag) is used to describe the combined effects of boundary layer normal pressure drag and surface friction drag. It is often convenient to combine these two forms of drag, as they both depend on the wing area and the dynamic pressure (l/2pV2). At constant altitude, both of these contributions to drag rise roughly with the square of the speed.