Calculation of Normal Shock-Wave Properties

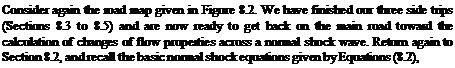
(8.6), and (8.10):

Continuity: pi «і = Р2И2 [8.2]

Momentum: p + plu2 = p2 + ргм2 [8.6]

Energy: h + у = h2 + у [8.10]

In addition, for a calorically perfect gas, we have

h2 = cpT2 [8.40]

p2 = p2RT2 [8.50]

Return again to Figure 8.3, and recall the basic normal shock-wave problem: given the conditions in region 1 ahead of the shock, calculate the conditions in region 2 behind the shock. Examining the five equations given above, we see that they involve five unknowns, namely, p2, u2, p2, h2, and T2. Hence, Equations (8.2), (8.6), (8.10), (8.49), and (8.50) are sufficient for determining the properties behind a normal shock wave in a calorically perfect gas. Let us proceed.

First, dividing Equation (8.6) by (8.2), we obtain

P1 , P 2 ,

——– h U ———– h u2

PU p2U2

P P2

——- — —– = W 2 — U1

PU p2U2

Recalling from Equation (8.23) that a = л/ур/р, Equation (8.51) becomes

Equation (8.52) is a combination of the continuity and momentum equations. The energy equation, Equation (8.10), can be used in one of its alternate forms, namely, Equation (8.35), rearranged below, and applied first in region 1 and then in region 2:

+ 1	У-1 2
[8.53]
2
and	[8.54]
2

In Equations (8.53) and (8.54), a* is the same constant value because the flow across the shock wave is adiabatic (see Sections 7.5 and 8.5). Substituting Equations (8.53) and (8.54) into Equation (8.52), we have

у + 1 а*2 у — 1 у + 1 а*2 у — 1

————— — ——- ц, ——————- _|_ —– до о

2 yu 2 у 2 уиг 2 у

У + 1 ч *2 , к – 1 ч

———- (u2-ui)a + ——(и2-иі)

2yuu2 2у

Dividing by и2 — мі, we obtain

Solving for a*, we obtain

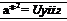[8.55]

Equation (8.55) is called the Prandtl relation and is a useful intermediate relation for normal shock waves. For example, from Equation (8.55),

и і и 2 a* a*

Recall the definition of characteristic Mach number, M* — и /a*, given in Section

8.4. Hence, Equation (8.56) becomes

1 = M*M*

* 1 , , or = [8.57]

2 M

Substituting Equation (8.48) into (8.57), we have

(у + V)M Г (у + l)M2 I 1 2 + (у — У)М L2 + (k-1)M2.

Solving Equation (8.58) for M, we obtain

Equation (8.59) is our first major result for a normal shock wave. Examine Equation

(8.59) closely; it states that the Mach number behind the wave M2, is a function only of the Mach number ahead of the wave M. Moreover, if M = 1, then M2 = 1. This is the case of an infinitely weak normal shock wave, defined as a Mach wave. Furthermore, if M > 1, then M2 < T, that is, the Mach number behind the normal shock wave is subsonic. As M increases above 1, the normal shock wave becomes stronger, and M2 becomes progressively less than 1. However, in the limit as M —у
oo, M2 approaches a finite minimum value, M2 V(K — l)/2y, which for air is 0.378.

Let us now obtain the ratios of the thermodynamic properties p2/pi, p2/pi, and T2/Tі across a normal shock wave. Rearranging Equation (8.2) and using Equation

(8.55) , we have

Pi _ u_ _ u] _ lP_ _

Pi u2 и2П] a*2 Substituting Equation (8.48) into (8.60), we obtain

P2 _ U_ __ (к + 1)M2 Pi m2 2 + (y – l)Aff

To obtain the pressure ratio, return to the momentum equation, Equation (8.6), com­bined with the continuity equation, Equation (8.2):

29 ? I ^2

Pl — Pl = PU — p2U2 = PU{U — U2) = PiMj I 1———

Ml

Dividing Equation (8.62) by pb and recalling that aj5 = ypi/pi, we obtain

For m2/mi in Equation (8.63), substitute Equation (8.61):

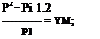
2+ (x – 1)M2_I

(K + 1)M2 J

Equation (8.64) simplifies to

To obtain the temperature ratio, recall the equation of state p = pRT. Hence,

[8.66]

Substituting Equations (8.61) and (8.65) into (8.66), and recalling that h = cpT, we obtain

Equations (8.61), (8.65), and (8.67) are important. Examine them closely. Note that p2/pi, pi/pi, and T2/T axe functions of the upstream Mach number M only. Therefore, in conjunction with Equation (8.59) for M2, we see that the upstream Mach number M is the determining parameter for changes across a normal shock wave in a

calorically perfect gas. This is a dramatic example of the power of the Mach number as a governing parameter in compressible flows. In the above equations, if Mi = 1, then рг/р = Рі/P = T2/T1 = 1; that is, we have the case of a normal shock wave of vanishing strength—a Mach wave. As M] increases above 1, pilp, Р2/p, and Тг/Т progressively increase above 1. In the limiting case of Mi —»• 00 in Equations

(8.59) , (8.61), (8.65), and (8.67), we find, for у = 1.4,

у — 1

——- = 0.378 (as discussed previously)

2 Y

Note that, as the upstream Mach number increases toward infinity, the pressure and temperature increase without bound, whereas the density approaches a rather moder­ate finite limit.

We have stated earlier that shock waves occur in supersonic flows; a stationary normal shock such as shown in Figure 8.3 does not occur in subsonic flow. That is, in Equations (8.59), (8.61), (8.65), and (8.67), the upstream Mach number is supersonic M] > 1. However, on a mathematical basis, these equations also allow solutions for Mi < 1. These equations embody the continuity, momentum, and energy equations, which in principle do not care whether the value of Mi is subsonic or supersonic. Here is an ambiguity which can only be resolved by appealing to the second law of thermodynamics (see Section 7.2). Recall that the second law of thermodynamics determines the direction which a given process can take. Let us apply the second law to the flow across a normal shock wave, and examine what it tells us about allowable values of Mi.

First, consider the entropy change across the normal shock wave. From Equation (7.25),

І2 P2

2+(y – DM? (Y + DM,[1]

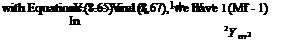
S2-S] = cp In — – R In — Ti p

obey the second law. However, if M < 1, then Equation (8.68) gives, v2 – ,V| < 0, which is not allowed by the second law. Consequently, in nature, only cases involving Mі > 1 are valid; that is, normal shock waves can occur only in supersonic flow.

Why does the entropy increase across the shock wave? The second law tells us that it must, but what mechanism does nature use to accomplish this increase? To answer these questions, recall that a shock wave is a very thin region (on the order of 1СГ5 cm) across which some large changes occur almost discontinuously. Therefore, within the shock wave itself, large gradients in velocity and temperature occur; that is, the mechanisms of friction and thermal conduction are strong. These are dissipative, irreversible mechanisms that always increase the entropy. Therefore, the precise entropy increase predicted by Equation (8.68) for a given supersonic M is appropriately provided by nature in the form of friction and thermal conduction within the interior of the shock wave itself.

In Section 7.5, we defined the total temperature 7b and total pressure po – What happens to these total conditions across a shock wave? To help answer this question, consider Figure 8.7, which illustrates the definition of total conditions ahead of and behind the shock. In region 1 ahead of the shock, a fluid element has the actual conditions of Mi, p[, T], and, sr. Now imagine that we bring this fluid element to rest isentropically, creating the “imaginary” state la ahead of the shock. In state la, the fluid element at rest would have a pressure and temperature po, and To. , respectively, that is, the total pressure and total temperature, respectively, in region 1. The entropy in state la would still be, V| because the fluid element is brought to rest isentropically; sia = Now consider region 2 behind the shock. Again consider a fluid element with the actual conditions of M2, p2. /2, and, s2, as sketched in Figure 8.7. And again let us imagine that we bring this fluid element to rest isentropically, creating the “imaginary” state 2a behind the shock. In state 2a, the fluid element at rest would

©

M2 < 1

Imaginary state 1 a where the fluid element has been brought to rest is­entropically. Thus, in state la, the pressure is p0,i (by definition). Entropy is still Si. Temperature is Tq і (by definition).

Figure 8.7 Total conditions ahead of and behind a normal shock wave.

have pressure and temperature po,2 and To,2, respectively, that is, the total pressure and total temperature, respectively, in region 2. The entropy in state 2a would still be S2 because the fluid element is brought to rest isentropically; ,s’2a = .s’2- The questions are now asked: How does To,2 compare with 7b, 1, and how does p0,2 compare with

Po, i?

To answer the first of these questions, consider Equation (8.30):

cpT1 + ^=cpT2 + £ 18.30]

From Equation (8.38), the total temperature is given by

u2

cpT0 = cpT + — [8.38]

Combining Equations (8.30) and (8.38), we have

cp7b, i = cpTo,2

Equation (8.69) states that total temperature is constant across a stationary normal shock wave. This should come as no surprise; the flow across a shock wave is adiabatic, and in Section 7.5 we demonstrated that in a steady, adiabatic, inviscid flow of a calorically perfect gas, the total temperature is constant.

To examine the variation of total pressure across a normal shock wave, write Equation (7.25) between the imaginary states la and 2a:

•S2a – Sla = Cp ІП ———- R ІП —- [8.70]

T a p la

However, from the above discussion, as well as the sketch in Figure 8.7, we have •?2a = S2, ria = 7га = 7b,2, 7)a — 7Ь, і, рга = Po,2, and pia = P0,. Thus, Equa­tion (8.70) becomes

From Equation (8.68), we know that S2 — si >0 for a normal shock wave. Hence, Equation (8.73) states that po,2 < Рол – The total pressure decreases across a shock wave. Moreover, since S2 — «і is a function of M only [from Equation (8.68)], then Equation (8.73) clearly states that the total pressure ratio ро, г/Po, across a normal shock wave is a function of M only.

.n. <N О Cl. ТЭ C Л (N 5

M!

Figure 8.8 The variation of properties across a normal shock wave as a function of upstream Mach number: у = 1.4.

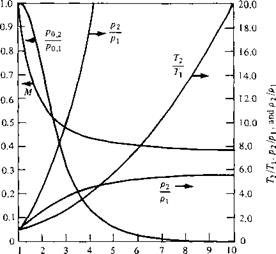
In summary, we have now verified the qualitative changes across a normal shock wave as sketched in Figure 7.4b and as originally discussed in Section 7.6. Moreover, we have obtained closed-form analytic expressions for these changes in the case of acalorically perfect gas. We have seen that p2/p, Pi/Pi, Ті/Ту М2, and рол/Рол are functions of the upstream Mach number M only. To help you obtain a stronger physical feeling of normal shock-wave properties, these variables are plotted in Figure

8.8 as a function of M. Note that (as stated earlier) these curves show how, as M becomes very large, T2/Ti and p2/p also become very large, whereas рг/p and M2 approach finite limits. Examine Figure 8.8 carefully, and become comfortable with the trends shown.

The results given by Equations (8.59), (8.61), (8.65), (8.67), and (8.73) are so important that they are tabulated as a function of M in Appendix В for у = 1 -4.

Consider a normal shock wave in air where the upstream flow properties are u = 680 m/s, T = 288 K, and />, = I atm. Calculate the velocity, temperature, and pressure downstream of the shock.

Solution

a, = У/ЛГ, = У 1.4(287)(288) = 340 m/s

u, _ 680 a/ ~ 340

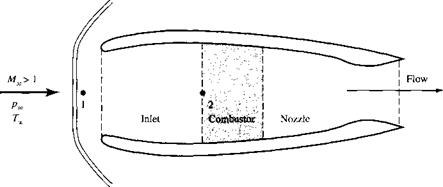
A ramjet engine is an air-breathing propulsion device with essentially no rotating machinery (no rotating compressor blades, turbine, etc.). The basic generic parts of a conventional ramjet are sketched in Figure 8.9. The flow, moving from left to right, enters the inlet, where it is compressed and slowed down. The compressed air then enters the combustor at very low subsonic speed, where it is mixed and burned with a fuel. The hot gas then expands through a nozzle. The net result is the production of thrust towards the left in Figure 8.9. In this figure the ramjet is shown in a supersonic freestream with a detached shock wave ahead of the inlet. The portion of the shock just to the left of point 1 is a normal shock. (A detached normal shock wave in front of the inlet of a ramjet in a supersonic flow is not the ideal operating condition; rather, it is desirable that the flow pass through one or more oblique shock waves before entering the inlet. Oblique shock waves are discussed in Chapter 9.) After passing through the shock wave, the flow from point 1 to point 2, located at the entrance to the combustor, is isentropic. The ramjet is flying at Mach 2 at a standard altitude of 10 km, where the air pressure and temperature are 2.65 x 104 N/m2 and 223.3 K, respectively. Calculate the air temperature and pressure at point 2 when the Mach number at that point is 0.2.

Solution

The total pressure and total temperature of the freestream at M= 2 can be obtained from Appendix A.

Po. oo = j Poo = (7.824)(2.65 x 104) = 2.07 x 10s N/m2

Figure 8.9 Schematic of a conventional subsonic-combustion ramjet engine.

To, c

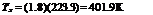
At point 1 behind the normal shock, the total pressure is, from Appendix B, for M-< = 2

Рол = ( — ) po. oc = (0.7209)(2.07 x 105) = 1.49 x 105 N/m2

VPo. cc/

The total temperature is constant across the shock, hence

To. і = T0,^ =401.9 К

The flow is isentropic between points 1 and 2, hence po and T0 are constant between these points. Therefore, p0,2 = 1.49 x 105 N/m2 and T0-2 = 401.9 K. At point 2, where M2 = 0.2, the ratios of the total-to-static pressure and total-to-static temperature, from Appendix A, are Рол/Pi = 1-028 and T02/T2 = 1.008. Hence,

At point 1, from Appendix В for = 10, we have

) (po. oo) = (0.3045 x 10_2)(1.125 x 109) = 3.43 x 106 N/m2

PO. oc /

At point 2, where M2 = 0.2, we have from Example 8.5, po, i/pi = 1.028 and T0,i/T2 Also at point 2, since the flow is isentropic between points 1 and 2,

p0,2 = Po. i = 3.43 x 106 N/m2 Ta, i = Год = 4690 К

Hence,

In atmospheres,

Compared to the rather benign conditions at point 2 existing for the case treated in Example 8.5, in the present example the air entering the combustor is at a pressure and temperature of 32.7 atm and 4653 К—both extremely severe conditions. The temperature is so hot that the fuel injected into the combustor will decompose rather than bum, with little or no thrust being produced. Moreover, the pressure is so high that the structural design of the combustor would have to be extremely heavy, assuming in the first place that some special heat-resistant material could be found that could handle the high temperature. In short, a conventional ramjet, where the flow is slowed down to a low subsonic Mach number before entering the combustor, will not work at high, hypersonic Mach numbers. The solution to this problem is not to slow the flow inside the engine to low subsonic speeds, but rather to slow it only to a lower but still supersonic speed. In this manner, the temperature and pressure increase inside the engine will be smaller and can be made tolerable. In such a ramjet, the entire flowpath through the engine remains at supersonic speed, including inside the combustor. This necessitates the injection and mixing of the fuel in a supersonic stream—a challenging technical problem. This type of ramjet, where the flow is supersonic throughout, is called a supersonic combustion ramjet—SCRAMjet for short. SCRAMjets are a current area of intense research and advanced development; at the time of writing no viable SCRAMjet engine has successfully powered a flight vehicle. This will soon change. SCRAMjet engines are the only viable airbreathing power plants for hypersonic cmise vehicles. Aspects of SCRAMjet engine design will be discussed in Chapter 9.