Circulation

Our heavyweight helicopter equal in the world does not have

In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]

The old plane — nonsense, pilots think - there was an attack

In spite of the fact that the main version of crash of the Russian plane of the Kogalymavia company [...]

You are reminded again that this is a tool-building chapter. Taken individually, each aerodynamic tool we have developed so far may not be particularly exciting. However, taken collectively, these tools allow us to obtain solutions for some very practical and exciting aerodynamic problems.

In this section, we introduce a tool which is fundamental to the calculation of aerodynamic lift, namely, circulation. This tool was used independently by Frederick Lanchester (1878-1946) in England, Wilhelm Kutta (1867-1944) in Germany, and Nikolai Joukowski (1847-1921) in Russia to create a breakthrough in the theory of aerodynamic lift at the turn of the twentieth century. The relationship between circulation and lift and the historical circumstances surrounding this breakthrough are discussed in Chapters 3 and 4. The purpose of this section is only to define circulation and relate it to vorticity.

Consider a closed curve C in a flow field, as sketched in Figure 2.36. Let V and ds be the velocity and directed line segment, respectively, at a point on C. The circulation, denoted by Г, is defined as

The circulation is simply the negative of the line integral of velocity around a closed curve in the flow; it is a kinematic property depending only on the velocity field and the choice of the curve C. As discussed in Section 2.2.8, Line Integrals, by mathematical convention the positive sense of the line integral is counterclockwise. However, in aerodynamics, it is convenient to consider a positive circulation as being clockwise.

Г = ~Фс V • ds

Figure 2.36 Definition of circulation.

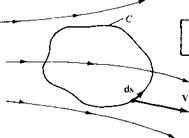
Hence, a minus sign appears in the definition given by Equation (2.136) to account for the positive-counterclockwise sense of the integral and the positive-clockwise sense of circulation.[4]

The use of the word “circulation” to label the integral in Equation (2.136) may be somewhat misleading because it leaves a general impression of something moving around in a loop. Indeed, according to the American Heritage Dictionary of the English Language, the first definition given to the word “circulation” is “movement in a circle or circuit.” However, in aerodynamics, circulation has a very precise technical meaning, namely, Equation (2.136). It does not necessarily mean that the fluid elements are moving around in circles within this flow field—a common early misconception of new students of aerodynamics. Rather, when circulation exists in a flow, it simply means that the line integral in Equation (2.136) is finite. For example, if the airfoil in Figure 2.26 is generating lift, the circulation taken around a closed curve enclosing the airfoil will be finite, although the fluid elements are by no means executing circles around the airfoil (as clearly seen from the streamlines sketched in Figure 2.26).

Circulation is also related to vorticity as follows. Refer back to Figure 2.9, which shows an open surface bounded by the closed curve C. Assume that the surface is in a flow field and the velocity at point P is V, where P is any point on the surface (including any point on curve C). From Stokes’ theorem [Equation (2.25)],

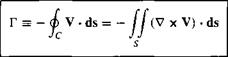[2.137]

Hence, the circulation about a curve C is equal to the vorticity integrated over any open surface bounded by C. This leads to the immediate result that if the flow is irrotational everywhere within the contour of integration (i. e., if V x V = 0 over any surface bounded by C), then Г = 0. A related result is obtained by letting the curve C shrink to an infinitesimal size, and denoting the circulation around this infinitesimally small curve by dT. Then, in the limit as C becomes infinitesimally small, Equation

(2.137) yields

dF = -(V x V) – dS = -(V x V) • ndS

where dS is the infinitesimal area enclosed by the infinitesimal curve C. Referring to Figure 2.37, Equation (2.138) states that at a point P in a flow, the component of vorticity normal to dS is equal to the negative of the “circulation per unit area,” where the circulation is taken around the boundary of dS.

For the velocity field given in Example 2.3, calculate the circulation around a circular path of radius 5 m. Assume that и and v given in Example 2.3 are in units of meters per second.

Solution

Since we are dealing with a circular path, it is easier to work this problem in polar coordinates, where x = r cosd, у = r sind, x2 + у2 = r2, Vr = и cost? + v sind, and Ve = —u sin# + vcosO. Therefore,

у r sin 9 sin 9

X2 + у2 г2 г

2тг m2/s
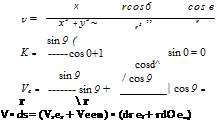