Conditions for Autorotation of Different Blade Elements

We have examined above the conditions for rotor autorotation as a function of blade element pitch and angle of attack. To facilitate our understanding of the problem, we assumed that all the blade elements operate under the same conditions, i. e., all the elements have the same incidence angles, velocities, the same forces AR, and the same inclination of these forces. But in reality,

each blade element operates under different autorotation conditions. Let us examine these conditions.

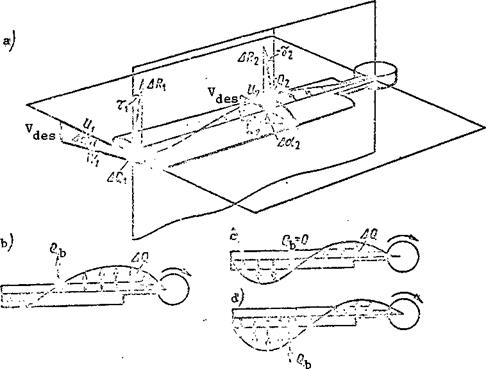
The angle of attack increment Act depends not only on the vertical rate of descent, but also on the circumferential velocity of the blade element.

The circumferential velocity is considerably higher for the tip elements than for the root elements; therefore, the angle of attack increment of the tip element is less than that of the root element, i. e., Aa^ < Aa^ (Figure 77a).

But then the elemental force vectors AR for the tip elements are inclined aft because of the low value of Да and create retarding moments. The blade tip elements usually operate in the decelerated autorotation regime. The retarding action of the tip elements is reduced by geometric twist of the blade but is not eliminated entirely.

The value of Да will be large for the root elements; therefore, the elemental force vectors AR will be tilted forward, and their projections AQ provide a turning moment. Consequently, the blade root elements operate under accelerated autorotation conditions. Since the blade tip elements retard the rotation while the root elements accelerate the rotation, what will be the operating regime of the entire rotor?

With reduction of the rotor pitch and with increase of the vertical rate of descent, the retarding action of the tip elements is less than the acceler­ating action of the root elements. The resultant of the elementary forces is directed forward, in the direction of rotor rotation and forms a turning moment (Figure 77b). In this case, the main rotor autorotation regime will be accelerated.

With increase of the pitch or reduction of the vertical rate of descent, the retarding action of the blade tip elements increases. If in this case the resultant of the elemental forces is zero, the rotor autorotation regime will be steady-state (Figure 77c). If the retarding action of the tip elements /124 exceeds the accelerating action of the root elements, the resultant of the

Figure 77. Autorotative conditions of different blade elements.

elementary forces is directed aft (Figure 77d) and creates a retarding moment. The rotor will operate in the decelerated autorotation regime.

Let us confirm these conclusions by an example.

Let r^ = 0.98; = 0.42; r^ “ 0.28.

The rotor blade twist Дф=4° is provided between the relative radii r = 0.3 – 0.5. The main rotor pitch is defined by the pitch of the blade

element with the relative radius r = 0.7.

The main rotor pitch for our example is ф = 4°. Then

The main rotor radius of the Mi-1 helicopter is R = 7.17 m. Then

/4 = 0.93-7.17 = 7 да; r2 = 0.42-7.17 = 3 m;

rs = 0,20 • 7,17

Let us find the circumferential velocities of the selected blade elements if

ш = 26 rad/sec; V, =8 m/sec. des

We find the angle of attack increments

Using the autorotation margin graph (see Figure 76), we find the auto­rotative regimes of the given blade elements. To this end we take three straight lines parallel to the abscissa axis, drawn through the ordinate points corresponding to the incidence angles го,=4°; ср2 = 3°; Su. The

point D in the figure corresponds to the blade tip element with the angle of attack <7..=6°o0” • This point lies in the decelerated autorotation regime ч. Сі — «к —о io ; . For this blade element the resultant aerodynamic force ДК. is tilted aft through the angle";’ — у— (u — 0.”) — — З la’ —0’15/ .

The point E, for which a-—(uc=T7’I5/, corresponds to the second blade element with the angle of attack :<2 — 12° . The pitch of this element is fj-j —0° . This means that this element is in the accelerated autorotation regime, and its aerodynamic force ДК. is tilted forward by the angle — ’. —’ — {••>. — n.-:)–— 15′ = -—The point B, for which n — corresponds to the third

blade element (angle of attack і ). The pitch of this element is

фЗ = о°. This element also is in the accelerated autorotation regime, hut its angle of attack is close to the stall angle, and the resultant aerodynamic force vector ДЫ is tilted forward through the angle — y — 3° — 9°30,= — .

The blade elements located closer to the hub axis will have angles of attack above the stall angle, i. e., they will operate under separated flow conditions. In our example, most of the blade elements operate under accelera­ted autorotation conditions, which means that the main rotor will operate in the accelerated autorotative regime.

In our example ш = 26 rad/sec or n = 250 rpm. For this rotor this rpm will be maximal, and further increase of the rpm is not permissible. The main rotor pitch must be increased to obtain the steady-state autorotative regime.

It is left to the reader to calculate for himself the approximate value of the pitch corresponding to this regime. The following comment must be added to what we have said. During flight in the autorotative regime, the helicopter will turn in the direction of rotation of the main rotor as a result of trans­mission shaft friction torque. In order to eliminate this turning, a thrust moment of the tail rotor, which turns under the influence of main rotor torque, must be created. Consequently, for steady-state autorotation the blades must create a small torque, which overcomes the friction torque in the transmission and the reactive torque of the tail rotor. We recall that the tail rotor creates thrust opposite in direction to the force which is generated in flight

with the engine operating (i. e., the tail rotor operates at small negative incidence angles; therefore, comparatively little driving torque is required).