Constant-Density Inviscid Flow

1- 1 Introduction

For the present chapter we adopt all the limitations listed in Section 1-1, plus the following:

(1) p = constant everywhere; and

(2) The fluid was initially irrotational.

The former assumption implies essentially an infinite speed of sound, while the latter guarantees the existence of a velocity potential. Turning to (1-74), we see that the flow field is now governed simply by Laplace’s equation

V4 = 0. (2-1)

Associated with this differential equation, the boundary conditions prescribe the values of the velocity potential or its normal derivative over the surfaces of a series of inner and outer boundaries. These conditions may be given in one of the following forms:

(1) The Neumann problem, in which vn = дФ/дп is given.

(2) The Dirichlet problem, in which the value of Ф itself is given.

(3) The mixed (Poincare) problem, in which Ф is given over certain portions of the boundary and дФ/дп is given over the remainder.

A great deal is known about the solution of classical boundary-value problems of this type and more particularly about fluid dynamic applica­tions. Innumerable examples can be found in books like Lamb (1945) and Milne-Thompson (1960). The subject is by no means closed, how­ever, as will become apparent in the light of some of the applications presented in later sections and chapters. A useful recent book, which combines many results of viscous flow theory with old and new develop­ments on the constant-density inviscid problem, is the one edited by Thwaites (1960).

Among the very many concepts and practical solutions that might be considered worthy of presentation, we single out here a few which are especially fundamental and which will prove useful for subsequent work.

21

2- 2 The Three-Dimensional Rigid Solid Moving Through a Liquid

Let us consider a single, finite solid S moving through a large mass of constant-density fluid with an outer boundary 2, which may for many purposes be regarded as displaced indefinitely toward infinity. For much of what follows, S may consist of several three-dimensional solids rather than a single one. The direction of the normal vector n will now be re­garded as from the boundary, either the inner boundary S or the outer boundary 2, toward the fluid volume.

In the early sections of Chapter 3, Lamb (1945) proves the following important but relatively straightforward results for a noncirculatory flow, which are stated here without complete demonstrations:

(1) The flow pattern is determined uniquely at any instant if the boundary values of Ф or дФ/дп are given at all points of S and 2. One important special case is that of the fluid at rest remote from <S; then Ф can be equated to zero at infinity.

(2) The value of Ф cannot have a maximum or minimum at any interior point but only on the boundaries. To be more specific, the mean value of Ф over any spherical surface containing only fluid is equal to the value at the center of this sphere. This result is connected with the interpreta­tion of the Laplacian operator itself, which may be regarded as a measure of the “lumpiness” of the scalar field; Laplace’s equation simply states that this “lumpiness ” has the smallest possible value in any region.

(3) The magnitude of the velocity vector Q = |Q| cannot have a max­imum in the interior of the flow field but only on the boundary. It can have a minimum value zero at an interior stagnation point.

(4) If Ф = 0 or дФ/дп = 0 over all of S and 2, the fluid will be at rest everywhere. That is, no boundary motion corresponds to no motion in the interior.

Next we proceed to derive some less straightforward results.

1. Green’s Theorem. For the moment, let the outer boundary of the flow field remain at a finite distance. We proceed from Gauss’ theorem for any vector field A, (1-14),

j^A-ndS = – jjjv ■ AdV. (2-2)

S+S V

(The minus sign here results from the reversal of direction of the normal vector.) Let Ф and Ф’ be two continuous functions with finite, single­valued first and second derivatives throughout the volume V. We do not yet specify that these functions represent velocity potentials of a fluid flow. Let

///[v*.

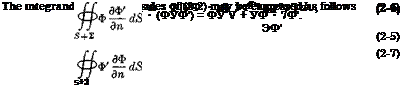Equations (2-4) and (2-5) are now substituted into Gauss’ theorem. After writing the result, we interchange the functions Ф and Ф’, obtaining two alternative forms of the theorem:

2. Kinetic Energy. As a first illustration of the application of Green’s theorem, let Ф in (2-6) be the velocity potential of some flow at a certain instant of time and let Ф’ = Ф. Of course, it follows that

у2Ф = VV = 0.

We thus obtain a formula for the integral of the square of the fluid particle speed throughout the field

“ -///lvt>’dr – "///«*"• 0«>

S+2 V V

Moreover, if we multiply the last member of (2-9) by one-half the fluid density p and change its sign, we recognize the total kinetic energy T of the fluid within V. There results

S+2

Such an integral over the boundary is often much easier to evaluate than a triple integral throughout the interior of the volume. In particular, ЭФ/дп is usually known from the boundary conditions. If the solid S is moving through an unlimited mass of fluid, with Q = 0 at infinity, it is a simple matter to prove that the integral over S vanishes. It follows that (2-10) need be integrated over only the inner boundary at the surface of the solid itself,

s

3. A Reciprocal Theorem. Another interesting consequence of Green’s theorem is obtained by letting Ф and Ф’ be the velocity potentials of two different constant-density flows having the same inner and outer bounding surfaces. Then, of course, the two Laplacians in (2-6) and (2-7) vanish, and the right-hand sides of these two relations are found to be equal. Equating the left-hand sides, we deduce

<2-,2)

S+S S+2

4. The Physical Interpretation of Ф. To assist in understanding the significance of the last two results and to give a meaning to the velocity potential itself, we next demonstrate an artificial but nevertheless meaning­ful interpretation of Ф. We begin with Bernoulli’s equation in the form (1-63), assuming the fluid at infinity to be at rest and evaluating the pres­sure integral in consequence of the constancy of p,

Imagine a process in which a system of very large impulsive pressures P = Ґ p dr (2-14)

is applied to the fluid, starting from rest, to produce the actual motion existing at a certain time t. In (2-14), т is a dummy variable of integration. We can make the interval of application of this impulse arbitrarily short, and integrate Bernoulli’s equation over it. [Incidentally, the same result is obtainable from the basic equations of fluid motion, (1-3) and (1-4), by a similar integration over the interval dt.] In the limit, the integrals of the pressure p„, pQ2/2, and p(Sl„ — fi) become negligible relative to that of the very large p, and we derive

pf = “p – (2-15)

J u-bt) от

Hence, P = — рф constitutes precisely the system of impulsive pressures required to generate the actual motion swiftly from rest. This process might be carried out, for example, by applying impulsive force and torque to the solid body and simultaneously a suitable distribution of impulsive pressures over the outer boundary 2. The total impulse thus applied will equal the total momentum in the instantaneous flow described by Ф. Unfortunately, both this momentum and the impulse applied at the outer boundary become indeterminate as 2 spreads outward toward infinity, so

that there are certain problems of physical interpretation when dealing with an externally unbounded mass of liquid.

In the light of this interpretation of the velocity potential, we reexamine the kinetic energy in (2-11), rewriting this result

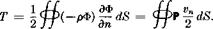(2-16)

The work done by an impulse acting on a system which starts from rest is known to be the integral over the boundary of the product of the impulse by one-half the final normal velocity at the boundary. Thus, the starting impulses do a total amount of work given by exactly the last member of (2-16). Since the system is a conservative one, this integral would be expected to equal the change of kinetic energy which, of course, is the final kinetic energy T in the present case. The difficulty in connection with carrying 2 to infinity disappears here, since the work contribution at the outer boundary can be shown to approach zero uniformly. Hence, the kinetic energy of an unbounded mass of constant-density fluid without circulation can be determined entirely from conditions at the inner bound­ary, and it will always be finite if the fluid is at rest at infinity.

The reciprocal theorem, (2-12), can be manipulated, by multiplication with the density, into the form

(2-17)

As such, it becomes a special case of a fairly familiar theorem of dynamics which states that, for any two possible motions of the same system, the sum over all the degrees of freedom of the impulse required to generate one motion multiplied by the velocity in the second motion equals the same summed product taken with the impulses and velocities interchanged.

One final important result is stated without proof: it can be shown that for a given set of boundary conditions the kinetic energy Г of a liquid in a finite or infinite region is a minimum when the flow is acyclical and irrotational, relative to all other possible motions.