Continuity Equation

In Section 2.3, we discussed several models which can be used to study the motion of a fluid. Following the philosophy set forth at the beginning of Section 2.3, we now apply the fundamental physical principles to such models. Unlike the above derivation of the physical significance of V • V wherein we used the model of a moving finite control volume, we now employ the model of a fixed finite control volume as sketched on the left side of Figure 2.11. Here, the control volume is fixed in space, with the flow moving through it. Unlike our previous derivation, the volume V and control surface S are now constant with time, and the mass of fluid contained within the control volume can change as a function of time (due to unsteady fluctuations of the flow field).

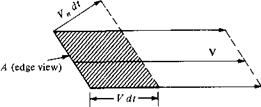
Before starting the derivation of the fundamental equations of aerodynamics, we must examine a concept vital to those equations, namely, the concept of mass flow. Consider a given area A arbitrarily oriented in a flow field as shown in Figure 2.16. In Figure 2.16, we are looking at an edge view of area A. Let A be small enough such that the flow velocity V is uniform across A. Consider the fluid elements with velocity V that pass through A. In time dt after crossing A, they have moved a distance V dt and have swept out the shaded volume shown in Figure 2.16. This volume is equal to the base area A times the height of the cylinder V„ dt, where V„ is the component of velocity normal to A; i. e.,

Volume = (V„dt)A

The mass inside the shaded volume is therefore

Mass = p(Vn dt)A

This is the mass that has swept past A in time dt. By definition, the mass flow through A is the mass crossing A per second (e. g., kilograms per second, slugs per second). Let m denote mass flow. From Equation (2.42).

. p{Vndt)A

m =——— :——

Equation (2.43) demonstrates that mass flow through A is given by the product

A related concept is that of mass flux, defined as the mass flow per unit area.

Typical units of mass flux are kg/(s • m2) and slug/(s • ft2).

The concepts of mass flow and mass flux are important. Note from Equation

(2.44) that mass flux across a surface is equal to the product of density times the component of velocity perpendicular to the surface. Many of the equations of aero­dynamics involve products of density and velocity. For example, in cartesian coor­dinates, V = Vxi + Vyj + Т, к = ui + uj 4- i/jk, where u, v, and w denote the x, y, and z components of velocity, respectively. (The use of u, v, and w rather than Vx, Vy, and V, to symbolize the x, у, and z components of velocity is quite common in aerodynamic literature; we henceforth adopt the u, v, and w notation.) In many of the equations of aerodynamics, you will find the products pu, pv, and pw always remember that these products are the mass fluxes in the x, y, and z directions, re­spectively. In a more general sense, if V is the magnitude of velocity in an arbitrary direction, the product p V is physically the mass flux (mass flow per unit area) across an area oriented perpendicular to the direction of V.

We are now ready to apply our first physical principle to a finite control volume fixed in space.