Control Sensitivity and Overshoots in Rapid Pullups

When powerful, light longitudinal controls became available for tactical airplanes, the problems of oversensitivity, sluggishness, normal acceleration overshoots, and pilot – induced oscillations appeared. Airplane-pilot coupling, also called pilot-induced oscilla­tions, is properly dealt with as the combination of the dynamics of human pilots with that of their airplanes (see Chapter 21). However, oversensitivity, sluggishness, and overshoots may be understood in simpler terms, that of the airplane alone, without specifically in­volving pilot dynamics. A fundamental indicator of airplane-alone pitch response is the pitch rate transfer function for elevator or stabilizer control inputs (Figure 10.2). Under the usual constant-airspeed assumption, this function has a second-order denominator and a first-order numerator. Although a pure delay may be added, only three parameters are involved: the frequency and damping ratio of the second-order term and the time constant of the first-order term. A number of criteria on oversensitivity, sluggishness, and overshoots deal with this airplane-alone transfer function.

10.3.1 Equivalent Systems Methods

Equivalent systems or low-order approaches refer to fitting an airplane-alone transfer function to the complex dynamics of actual airplane and flight control systems. Hodgkinson, La Manna, and Hyde (1976) are generally referenced as the origin of the

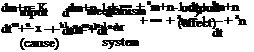A mechanism or complete system with input x and output y defined by the differential equation

can be represented by the transfer function in the Laplace variable s:

Y(s) _ K(sn + a1sn 1 + ••• + an-1s + an)

X(s) = sm+n + b1sm+n-1 + ••• + bm+n_ 1s + bm+n ^

An example is the pitch rate transfer function for elevator or stabilizer inputs, with the airspeed degree of freedom suppressed:

q(s) _ (Ms + ZsMw)s + ZsMw — MsZw

S(s) = s2 —(UoMw + Zw + Mq)s + MqZw — UoMw •

In these equations, a, b = constants K = gain

Ms, Zw, etc. = control and stability derivatives q = pitching velocity s = Laplace variable Uo = forward speed S = elevator or stabilizer deflection.

Figure 10.2 The transferfunction concept. (Adapted from AircraftDynamics andAutomatic Control, by McRuer, Ashkenas, and Graham, Princeton U. Press, 1973)

equivalent systems method. The McRuer, Ashkenas, and Graham approximate factors, with time delay added from variable stability NT-33 tests carried out by Dante DiFranco, were used to match frequency responses of the Neal-Smith data set.

Transfer function criteria, for the airplane alone or the equivalent system, have the authority of a great deal of analysis, simulator, and flight research. Excellent reviews of this field are given by Gibson (1995) and by Hoh and Mitchell (1996). While the original work on transfer-function-based criteria was concerned with tactical airplanes, these criteria were used as well in the flight control designs of modern transport airplanes such as the Boeing 777 (Ward, 1996) and the Airbus series, starting with the A320.