Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Control System Coupling with Elastic Modes
Coupling of the B-47’s yaw damper system with the airplane’s fuselage sidebending mode was resolved simply when the yaw damper’s rate gyro was relocated. That is, the rudder’s yaw damping action cut off at a low enough bandwidth that the side-bending mode itself was not reinforced.
The coupling of stability augmentation systems and airplane elastic modes takes on a new dimension for high-bandwidth control systems. If the flight control system is capable of interacting with the airplane’s structural modes, the stability of the combination must be assured. A conventional approach is gain stabilization, in which control system response at structural mode frequencies is attenuated by notch filters. The notch filters reduce rate gyro and accelerometer outputs in a narrow band around modal frequencies.
While effective, notch filtering invariably introduces lag at lower frequencies, which can adversely affect flying qualities. Phase stabilization (Ashkenas, Magdaleno, and McRuer, 1983) attempts to replace or supplement notch filtering by creating dipoles out of the
|
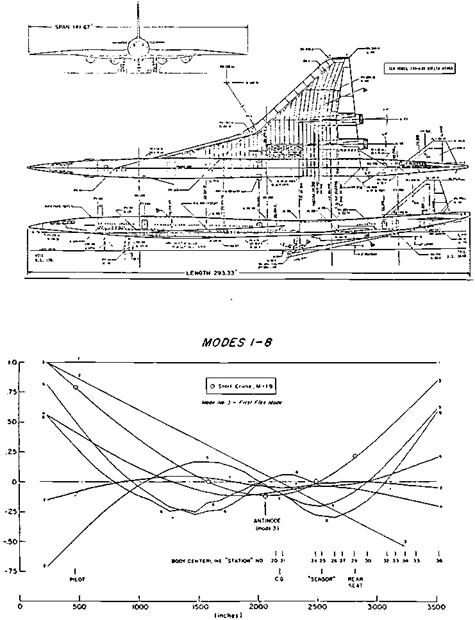
Figure 19.10 The first six normal modes at the centerline of a Boeing supersonic transport proposal, typical of the data used in the normal-mode method for the effect of aeroelasticity on stability and control. The modes are normalized in amplitude. Modes 1 and 2 are rigid-body plunge and pitch. (From Ashkenas, Magdaleno, and McRuer, NASA CR-172201, Aug. 1983) |
structural bending poles. The dipoles are the stable type referred to in the “Transfer Function Dipoles” section of Chapter 20, with the zero below the pole in the s-plane. Zero location for particular modes can be controlled by sensor location, but locations that produce stable dipoles for some modes will be wrong for others.
