Convergent-divergent nozzle

Let us now consider the flow through a contracting-expanding duct, a conver­gent-divergent nozzle, a de Laval nozzle – at any rate a constriction in a duct; or, as we called it in the low speed case, a venturi meter.

It is true that there are variations in the shapes of these devices according to what they are required to do, and according to the speed of flow with which they have to deal, but all have this in common – that they converge from the inlet to a throat, then diverge to the outlet.

We are familiar by now with the picture which illustrates subsonic flow through a venturi tube (Fig. 2.6); in the contracting portion the streamlines converge, the airflow accelerates, the pressure falls and, although the change in density is small (so small that we could then afford to neglect it), it is a decrease, i. e. the air is rarefied. In the expanding duct, beyond the throat, the streamlines diverge, the airflow decelerates, the pressure rises, and such small change in density as may occur is an increase, i. e. the air is compressed.

What happens if we gradually speed up the flow through the venturi tube? The reader can probably answer that from what we have discovered first about transonic flow, then about supersonic flow.

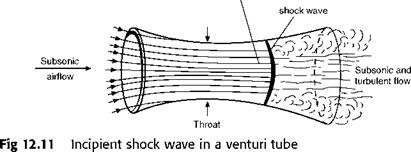
The first thing that will happen is that when the airflow, at the throat, reaches the speed of sound, a shock wave will be formed just beyond the throat just as it was on the camber of an aerofoil; so instead of the gradual rise in pressure and fall in speed beyond the throat, there will be a sudden rise in pressure, a sudden fall in speed, and the flow behind the shock wave will

Fig 12.10 Supersonic flow over double wedge at angle giving maximum L/D

become turbulent (Fig. 12.11). The front portion of the venturi will still func­tion reasonably like a venturi, i. e. the velocity will increase and the pressure fall, but the rear portion will no longer serve its proper purpose.

It is interesting to note that if the upstream flow is subsonic then at the throat the speed can never be greater than the speed of sound. If the flow does reach this speed it may then accelerate to supersonic speed downstream of the throat (Fig. 12.11). In this condition the duct is said to be choked. If the downstream pressure is reduced the supersonic region extends and the shock moves out of the divergent section.

If the flow in the duct ahead of the contraction is supersonic, we find that the flow behaves in the opposite way! This time the speed reduces in the con­vergent section and increases in the divergent section, reaching a minimum value at the throat (Fig. 12.12). The increase in speed is still, however, accom­panied by a decrease in pressure and vice versa.