Definition of Compressibility

All real substances are compressible to some greater or lesser extent; that is, when you squeeze or press on them, their density will change. This is particularly true of gases, much less so for liquids, and virtually unnoticeable for solids. The amount by which a substance can be compressed is given by a specific property of the substance called the compressibility, defined below.

Consider a small element of fluid of volume v, as sketched in Figure 7.3. The pressure exerted on the sides of the element is p. Assume the pressure is now in­creased by an infinitesimal amount dp. The volume of the element will change by a corresponding amount d v; here, the volume will decrease; hence, d v shown in Figure

7.3 is a negative quantity. By definition, the compressibility r of the fluid is

1 d v v dp

Physically, the compressibility is the fractional change in volume of the fluid element per unit change in pressure. However, Equation (7.33) is not precise enough. We know from experience that when a gas is compressed (say, in a bicycle pump), its temperature tends to increase, depending on the amount of heat transferred into or out of the gas through the boundaries of the system. If the temperature of the fluid element in Figure 7.3 is held constant (due to some heat transfer mechanism), then r is identified as the isothermal compressibility rt, defined from Equation (7.33) as

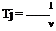
[7.34]

On the other hand, if no heat is added to or taken away from the fluid element, and if friction is ignored, the compression of the fluid element takes place isentropically, and t is identified as the isentropic compressibility rs, defined from Equation (7.33) as

1 /dv’

[7.35]

?s =

v dPJs

where the subscript 5 denotes that the partial derivative is taken at constant entropy. Both Xj and r, are precise thermodynamic properties of the fluid; their values for

Definition of compressibility.

different gases and liquids can be obtained from various handbooks of physical prop­erties. In general, the compressibility of gases is several orders of magnitude larger than that of liquids.

The role of the compressibility r in determining the properties of a fluid in motion is seen as follows. Define v as the specific volume (i. e., the volume per unit mass). Hence, v = 1 / p. Substituting this definition into Equation (7.33), we obtain

1 dp P dp

Thus, whenever the fluid experiences a change in pressure dp, the corresponding change in density dp from Equation (7.36) is

dp = p x dp

Consider a fluid flow, say, for example, the flow over an airfoil. If the fluid is a liquid, where the compressibility r is very small, then for a given pressure change dp from one point to another in the flow, Equation (7.37) states that dp will be negligibly small. In turn, we can reasonably assume that p is constant and that the flow of a liquid is incompressible. On the other hand, if the fluid is a gas, where the compressibility r is large, then for a given pressure change dp from one point to another in the flow, Equation (7.37) states that dp can be large. Thus, p is not constant, and in general, the flow of a gas is a compressible flow. The exception to this is the low-speed flow of a gas; in such flows, the actual magnitude of the pressure changes throughout the flow field is small compared with the pressure itself. Thus, for a low-speed flow, dp in Equation (7.37) is small, and even though r is large, the value of dp can be dominated by the small dp. In such cases, p can be assumed to be constant, hence allowing us to analyze low-speed gas flows as incompressible flows (such as discussed in Chapters 3 to 6).

Later, we demonstrate that the most convenient index to gage whether a gas flow can be considered incompressible, or whether it must be treated as compressible, is the Mach number M, defined in Chapter 1 as the ratio of local flow velocity V to the local speed of sound a:

V

M = — [7.38]

a

We show that, when M > 0.3, the flow should be considered compressible, Also, we show that the speed of sound in a gas is related to the isentropic compressibility rs, given by Equation (7.35).