Definition of Total (Stagnation) Conditions
At the beginning of Section 3.4, the concept of static pressure p was discussed in some detail. Static pressure is a measure of the purely random motion of molecules in a gas; it is the pressure you feel when you ride along with the gas at the local flow velocity. In contrast, the total (or stagnation) pressure was defined in Section 3.4 as the pressure existing at a point (or points) in the flow where V = 0. Let us now define the concept of total conditions more precisely.
Consider a fluid element passing through a given point in a flow where the local pressure, temperature, density, Mach number, and velocity are p, T, p, M, and V, respectively. Here, p, T, and p are static quantities (i. e., static pressure, static
temperature, and static density, respectively); they are the pressure, temperature, and density you feel when you ride along with the gas at the local flow velocity. Now imagine that you grab hold of the fluid element and adiabatically slow it down to zero velocity. Clearly, you would expect (correctly) that the values of p, T, and p would change as the fluid element is brought to rest. In particular, the value of the temperature of the fluid element after it has been brought to rest adiabatically is defined as the total temperature, denoted by Tq. The corresponding value of enthalpy is defined as the total enthalpy h0, where ho = cpT0 for a calorically perfect gas. Keep in mind that we do not actually have to bring the flow to rest in real life in order to talk about the total temperature or total enthalpy; rather, they are defined quantities that would exist at a point in a flow if (in our imagination) the fluid element passing through that point were brought to rest adiabatically. Therefore, at a given point in a flow, where the static temperature and enthalpy are T and h, respectively, we can also assign a value of total temperature To and a value of total enthalpy ho defined as above.
For such a flow, Equation (7.56) can be used as a form of the governing energy equation.
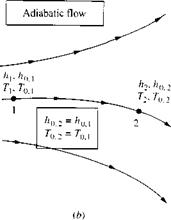
Keep in mind that the above discussion marbled two trains of thought: On the one hand, we dealt with the general concept of an adiabatic flow field [which led to Equations (7.51) to (7.53)], and on the other hand, we dealt with the definition of total enthalpy [which led to Equation (7.54)]. These two trains of thought are really separate and should not be confused. Consider, for example, a general nonadiabatic flow, such as a viscous boundary layer with heat transfer. A generic non-adiabatic flow is sketched in Figure 7.4a. Clearly, Equations (7.51) to (7.53) do not hold for such a flow. However, Equation (7.54) holds locally at each point in the flow, because the assumption of an adiabatic flow contained in Equation (7.54) is made through the definition of ho and has nothing to do with the general overall flow field. For example, consider two different points, 1 and 2, in the general flow, as shown in Figure 7.4a. At point 1, the local static enthalpy and velocity are h i and V, respectively. Hence, the local total enthalpy at point 1 is ho, і = h + V2/2. At point 2, the local static enthalpy and velocity are h2 and V2, respectively. Hence, the local total enthalpy at point 2 is hop = h2+ V}/2. If the flow between points 1 and 2 is nonadiabatic, then ho, Ф hop. Only for the special case where the flow is adiabatic between the two points would ho, — ho<2. This case is illustrated in Figure l. Ab. Of course, this is the special case treated by Equations (7.55) and (7.56).
Return to the beginning of this section, where we considered a fluid element passing through a point in a flow where the local properties are p. T, p, M, and V. Once again, imagine that you grab hold of the fluid element and slow it down to zero velocity, but this time, let us slow it down both adiabatically and reversibly. That is, let us slow the fluid element down to zero velocity isentropically. When the fluid element is brought to rest isentropically, the resulting pressure and density are defined as the total pressure po and total density po. (Since an isentropic process is also adiabatic, the resulting temperature is the same total temperature Го as discussed earlier.) As before, keep in mind that we do not have to actually bring the flow to rest in real life in order to talk about total pressure and total density; rather, they are defined quantities that would exist at a point in a flow if (in our imagination) the fluid element passing through that point were brought to rest isentropically. Therefore, at a given point in a flow, where the static pressure and static density are p and p, respectively, we can also assign a value of total pressure po, and total density po defined as above.
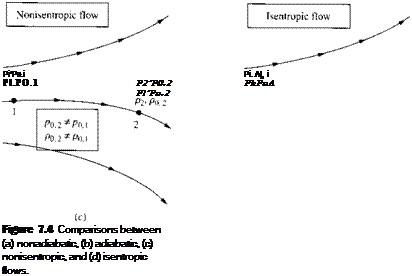
The definition of po and po deals with an isentropic compression to zero velocity. Keep in mind that the isentropic assumption is involved with the definition only. The concept of total pressure and density can be applied throughout any general nonisentropic flow. For example, consider two different points, 1 and 2, in a general
 |

![]()
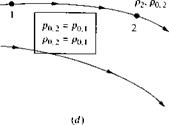
flow field, as sketched in Figure 7.4c. At point 1, the local static pressure and static density are p and f>, respectively; also the local total pressure and total density are Po. i and (>{) і, respectively, defined as above. Similarly, at point 2, the local static pressure and static density are p2 and /ь. respectively, and the local total pressure and total density are po,2 and po.2. respectively. If the flow is nonisentropic between points 1 and 2, then p0.i ф p0 2 and po. i ф Ли, as shown in Figure 7.4c. On the other hand, if the flow is isentropic between points 1 and 2, then po. i = Po,2 and Po. i = Po.2, as shown in Figure 7.4d. Indeed, if the general flow field is isentropic throughout, then both po and po are constant values throughout the flow.
As a corollary to the above considerations, we need another defined temperature, denoted by T*, and defined as follows. Consider a point in a subsonic flow where the local static temperature is T. At this point, imagine that the fluid element is
speeded up to sonic velocity, adiabatically. The temperature it would have at such sonic conditions is denoted as T*. Similarly, consider a point in a supersonic flow, where the local static temperature is T. At this point, imagine that the fluid element is slowed down to sonic velocity, adiabatically. Again, the temperature it would have at such sonic conditions is denoted as T*. The quantity T* is simply a defined quantity at a given point in a flow, in exactly the same vein as T0, p0, and p0 are defined quantities. Also, a* = yJyRT*.











