Diagram of Forces Acting on Helicopter and Hovering Conditions

In the further study of the hovering regime we examine helicopter hovering relative to the air with the main rotor operating in the axial flow regime.

In order to avoid complicating our understanding of the question, we shall assume that the wind velocity is zero.

During hovering, it is necessary to observe the general conditions which /75 characterize any steady-state flight regime, i. e.,

£F =0 and ZM = 0. eg eg

The following basic forces act on the helicopter during hovering (Figure 53a):

Figure 53. Forces acting on helicopter in hovering regime.

helicopter weight G;

main rotor thrust T;

tail rotor thrust T ;

t. r

parasite drag X

The parasite drag force arises as a result of air flow from the main

rotor over the fuselage and other parts of the helicopter. This force is

very small and amounts to about 1-2% of the helicopter weight. The main

rotor thrust increases somewhat as a result of the air flow over the fuselage,

which means that the effect of the force X decreases, and it can hereafter

par

be neglected.

The main rotor reactive moment during hovering is balanced by the tail rotor thrust moment = T L. This is necessary to prevent the helicopter from turning about the vertical axis. But in this case the unbalanced force T r acts on the helicopter and the helicopter displaces to the side. To prevent lateral displacement it is necessary to balance the tail rotor thrust by a force directed oppositely. To this end the main rotor thrust vector is deflected to the side opposite the direction of the tail rotor thrust. For helicopters with right hand rotation of the main rotor (as seen from above) the tail rotor thrust is directed to the left (Figure 53b). As a result of tilting of the cone axis to the right through the angle 6, the main rotor side thrust develops 110

Ss — Г sin 8,

which balances the tail rotor thrust. The vertical component Y=TCOS d of the main rotor thrust will be balanced by the helicopter weight.

The angle 6 does not exceed 3-5°. And since COs5°!^i, we can say with /75 adequate precision that У Я# T. Thus, the helicopter hovering conditions are expressed by the equalities

Y = G or Y – G = 0,

Since there are no forces acting along the helicopter longitudinal axis in the hovering regime, EM = 0 is assured.

In view of the equality Y~T we can write the first hovering regime condition in the form T = G. We shall use this equality hereafter. There­fore, for helicopter hovering it is necessary that:

T = G (constant hovering height);

T = S (absence of lateral displacement);

L » Г S

EM = 0 (absence of rotation about the center of gravity).

The hovering regime is a characteristic flight regime and defines to a considerable degree the helicopter’s flight characteristics.

Example. A helicopter is hovering. G = 2200 kgf, = 575 hp, t, = 0.78,

n = 249 rpm, L = 8.65 m. Find: N, M, T, and S.

t. r ’ r t. r

Solution. 1. The power expended in rotating the main rotor is defined with account for the power utilization coefficient

N = N£ = 575 XO 78 = 450 bp.

2. From (11) we find the main rotor reactive moment M = r.

r —

Ш

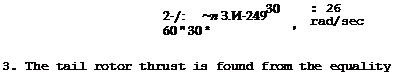The main rotor angular velocity is found from the formula

-i2ff-150k8£-

t. r

4. The tilt of the thrust vector is found from the equality

150

2200

arcsin 0.068 = 4°,