Doublet Flow: Our Third Elementary Flow

There is a special, degenerate case of a source-sink pair that leads to a singularity called a doublet. The doublet is frequently used in the theory of incompressible flow; the purpose of this section is to describe its properties.

Consider a source of strength Л and a sink of equal (but opposite) strength —A separated by a distance /, as shown in Figure 3.24a. At any point P in the flow, the stream function is

A A r ,

t/r = —(0, – в2) =———— Ав [3.84]

2jt 2jt

where Ав = 02 — в as seen from Figure 3.24a. Equation (3.84) is the stream func­tion for a source-sink pair separated by the distance /.

Now in Figure 3.24a, let the distance / approach zero while the absolute magni­tudes of the strengths of the source and sink increase in such a fashion that the product lA remains constant. This limiting process is shown in Figure 3.24b. In the limit, as / -> 0 while lA remains constant, we obtain a special flow pattern defined as a doublet. The strength of the doublet is denoted by к and is defined as к = l A. The stream function for a doublet is obtained from Equation (3.84) as follows:

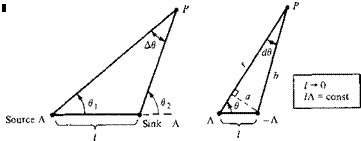where in the limit A6 d6 -> 0. (Note that the source strength A approaches an infinite value in the limit.) In Figure 3.24i>, let r and b denote the distances to point P from the source and sink, respectively. Draw a line from the sink perpendicular to r, and denote the length along this line by a. For an infinitesimal dG, the geometry

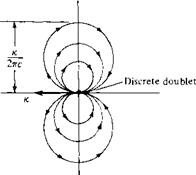
is a circle with a diameter d on the vertical axis and with the center located d/2 directly above the origin. Comparing Equations (3.89) and (3.90), we see that the streamlines for a doublet are a family of circles with diameter к/Ътс, as sketched in Figure 3.25. The different circles correspond to different values of the parameter c. Note that in Figure 3.24 we placed the source to the left of the sink; hence, in Figure 3.25 the direction of flow is out of the origin to the left and back into the origin from the right. In Figure 3.24, we could just as well have placed the sink to the left of the source. In such a case, the signs in Equations (3.87) and (3.88) would be reversed, and the flow in Figure 3.25 would be in the opposite direction. Therefore, a doublet has associated with it a sense of direction—the direction with which the flow

moves around the circular streamlines. By convention, we designate the direction of the doublet by an arrow drawn from the sink to the source, as shown in Figure 3.25. In Figure 3.25, the arrow points to the left, which is consistent with the form of Equations (3.87) and (3.88). If the arrow would point to the right, the sense of rotation would be reversed, Equation (3.87) would have a positive sign, and Equation (3.88) would have a negative sign.

Returning to Figure 3.24, note that in the limit as l —> 0, the source and sink fall on top of each other. However, they do not extinguish each other, because the absolute magnitude of their strengths becomes infinitely large in the limit, and we have a singularity of strength (oo — oo); this is an indeterminate form which can have a finite value.

As in the case of a source or sink, it is useful to interpret the doublet flow shown in Figure 3.25 as being induced by a discrete doublet of strength к placed at the origin. Therefore, a doublet is a singularity that induces about it the double-lobed circular flow pattern shown in Figure 3.25.