Entropy and the Second Law of Thermodynamics

Consider a block of ice in contact with a red-hot plate of steel. Experience tells us that the ice will warm up (and probably melt) and the steel plate will cool down. However, Equation (7.11) does not necessarily say this will happen. Indeed, the first law allows that the ice may get cooler and the steel plate hotter—just as long as energy is conserved during the process. Obviously, in real life this does not happen; instead, nature imposes another condition on the process, a condition that tells us which direction a process will take. To ascertain the proper direction of a process, let us define a new state variable, the entropy, as follows:

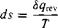[7.13]

where. s’ is the entropy of the system, Sq, cv is an incremental amount of heat added reversibly to the system, and T is the system temperature. Do not be confused by the above definition. It defines a change in entropy in terms of a reversible addition of heat SqKv. However, entropy is a state variable, and it can be used in conjunction with any type of process, reversible or irreversible. The quantity SqKV in Equation

(7.13) is just an artifice; an effective value of SqKy can always be assigned to relate the initial and end points of an irreversible process, where the actual amount of heat

added is 8q. Indeed, an alternative and probably more lucid relation is

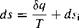[7.14]

In Equation (7.14), &q is the actual amount of heat added to the system during an actual irreversible process, and dsmv is the generation of entropy due to the irreversible, dis­sipative phenomena of viscosity, thermal conductivity, and mass diffusion occurring within the system. These dissipative phenomena always increase the entropy:

[7.15]

In Equation (7.15), the equals sign denotes a reversible process, where by definition no dissipative phenomena occur within the system. Combining Equations (7.14) and

(7.15) , we have

[7.16]

Furthermore, if the process is adiabatic, &q = 0, and Equation (7.16) becomes

[7.17]

Equations (7.16) and (7.17) are forms of the second law of thermodynamics. The second law tells us in what direction a process will take place. A process will proceed in a direction such that the entropy of the system plus that of its surroundings always increases or, at best, stays the same. In our example of the ice in contact with hot steel, consider the system to be both the ice and steel plate combined. The simultaneous heating of the ice and cooling of the plate yield a net increase in entropy for the system. On the other hand, the impossible situation of the ice getting cooler and the plate hotter would yield a net decrease in entropy, a situation forbidden by the second law. In summary, the concept of entropy in combination with the second law allows us to predict the direction that nature takes.

The practical calculation of entropy is carried out as follows. In Equation (7.12), assume that heat is added reversibly; then the definition of entropy, Equation (7.13), substituted in Equation (7.12) yields

T ds — p dv = de

From the definition of enthalpy, Equation (7.3), we have

dh = de + p dv + v dp

Combining Equations (7.18) and (7.19), we obtain

T ds — dh — v dp	[7.20]

Equations (7.18) and (7.20) are important; they are essentially alternate forms of the first law expressed in terms of entropy. For a perfect gas, recall Equations (7.5a and b), namely, de = cvdT and dh = cp dT. Substituting these relations into Equations

(7.18) and (7.20), we obtain

dT pdv

ds = cv— + — [7.21]

dT v dp

and ds=c„—————— [7.22]

p T t

Working with Equation (7.22), substitute the equation of state pv = RT, or v/T = R/p, into the last term:

ds=c„———- R— [7.23]

T P

Consider a thermodynamic process with initial and end states denoted by 1 and 2, respectively. Equation (7.23), integrated between states 1 and 2, becomes

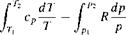[7.24]

For a calorically perfect gas, both R and cp are constants; hence, Equation (7.24) becomes

In a similar fashion, Equation (7.21) leads to

Equations (7.25) and (7.26) are practical expressions for the calculation of the entropy change of a calorically perfect gas between two states. Note from these equations that 5 is a function of two thermodynamic variables, for example, 5 = s(p, T), s = 5(u, T).