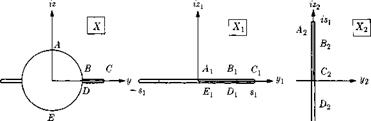
Examples of Lifting Slender-Body Flow

A particularly fortunate consequence of the equivalence rule is that the outer flow is needed only for the calculation of g(x), which is a symmetric term that only influences the drag but not transverse forces and moments. For the calculation of lifting flows one therefore seeks the inner constant – density two-dimensional crossflow which is independent of the Mach number and which may be obtained, for example, by using complex variables. Some of the results of the classical two-dimensional theory may be directly applied. Thus, the flow around a circular cylinder applies to the lifting slender body of revolution, and the solution for a flat plate normal to the stream can be used for the flow around a thin, slender wing. A simple, yet practically useful configuration that incorporates these as special cases is that of a mid-winged body of revolution (see Fig. 6-3).

Fig. 6-3. Wing-body configuration.

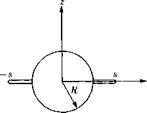
To determine the perturbation velocity potential (</> = е2Фг2 in this case) it is, in this problem, convenient to align the x-axis with the body axis and let the free-stream vector be inclined by the angle a to the x-axis. That we then consider the flow in cross sections normal to the body axis instead of normal to the free stream will only introduce differences of order a2, which will be negligible in the present approximation; they will only be of importance for the calculation of higher-order terms. The prob­lem becomes that of finding a two-dimensional constant-density flow having a nondimensional vertical velocity of

W

= sin a ~ a (6-57)

U со

at infinity and zero normal velocity component at the body contour. Let the velocity potential corresponding to this flow be <p’:

tp’ = ip + az. (6-58)

We may obtain <p’ from a complex potential:

W'(X) = V'(y, z) + гф'(у, z), (6-59)

where

X = у + iz. (6-60)

The complex potential W’ will be constructed in steps using conformal transformation. First, the Joukowsky transformation

Хг = X + R2/X (6-61)

maps the outside of the contour onto the outside of a slit along the у i-axis (see Fig. 6-4) of width 2s i, where

E2 Fig. 6-4. Mapping of wing-body cross section onto a slit.

Corresponding points are marked in the figure. A second transformation

X2 = (Xf – sf)112 (6-63)

transforms the horizontal slit to a vertical slit of width 2s i. Since in both transformations the plane remains undistorted at infinity, the flow in the X2-plane is simply

V?'(X2) = – iaX2, (6-64)

that is, an undisturbed vertical flow of (nondimensional) velocity a. By substituting (6-61)-(6-63) into (6-64) we obtain

V?'(X)

Thus for the complex velocity perturbation potential,

W(X) = V?'(X) + iaX = – ia

This solution was given by Spreiter (1950). It is a straightforward process to derive from it the cases of body alone (R — s) and wing along (R = 0).

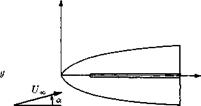
It is interesting to note that the crossflow considered above has no physical significance in a truly two-dimensional case, since then the flow will separate and the flow becomes rotational and nonpotential. In the slender-body case the axial flow keeps the crossflow from separating so that the potential-flow solution gives a realistic result. However, for large angles of attack the flow will separate, particularly when the aspect ratio is very small. The type of flow that then will be encountered is illustrated in Fig. 6-5. The flow separates at the leading edges and forms two station­ary, more-or-less concentrated vortices above the wing. Separation gives rise to an additional “drag” in the crossflow plane, which is equivalent to

Fig. 6-5. Leading-edge separation on | j

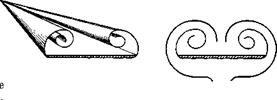a slender wing. T 1

increased lift and drag on the vehicle. Simplified models of this type of flow have been considered by, among others, Bollay (1937), Legendre (1952), and Mangier and Smith (1956).

The calculation of total lift and moments on slender bodies will be considered in Section 6-7.