Expansion in a Small Parameter; Singular Perturbation Problems

As will be seen, the majority of the problems that will be considered subsequently are characterized mathematically by the property that, in the limit as the small parameter vanishes, one or more highest-order – derivative terms in the governing differential equation drop out so that the differential equation degenerates. Hence not all of the original bound­ary conditions of the problem can be satisfied. This type of problem is known as a singular perturbation problem. In recent years a very powerful system­atic method to treat such problems has been developed by the Caltech school, primarily by Kaplun (1954, 1957) and Lagerstrom (1957).[5] The method is known by various names; the most frequently used one is “the inner and outer expansion method.” Another one is “the method of matched asymptotic expansions” suggested by Bretherton (1962). This name has been adopted in a recent book by Van Dyke (1964) and we will follow here his usage of terminology. The reader is referred to this book for more details on the method.

In order to introduce the method and its basic ideas we will first, as is customary in the literature on the subject [see, e. g.,

Erdelyi (1961)], consider a simple prob – Impulse I lem involving only an ordinary differen­tial equation. The problem chosen may be stated in physical terms as follows:

“Given a mass m on a spring of spring con­stant к with a viscous damper of damping

equation and the associated boundary conditions are

constant d. (See Fig. 3-2.) At time t = 0 the mass is given an impulse I (for example, by shooting off a charge to the left). What is the subsequent motion of the mass when tn is very small?”* This problem will be solved in essentially three different ways. First, an exact solution may easily be obtained. The governing differential

This will be the reference solution used in assessing the approximate solutions that follow.

We shall now obtain an approximate solution valid for small mass m by use of simple physical reasoning. From the boundary condition (3-2) it follows that the initial velocity will be very high for small m, hence the dumping force will be the main decelerating force in the initial stages. The restoring force due to the spring, on the other hand, will be com­paratively much smaller because initially x is small. Therefore, the initial motion of the mass is governed approximately by the following equation:

The mass will have reached its maximum deviation when u(t) = 0. From (3-7) we thus obtain, approximately,

After the mass has reached its maximum deviation, the spring will force it relatively slowly back to its original position. Since the mass is so small, the motion will then be dominated by the spring and the damper. Conse­quently, the following equation will approximately describe its subsequent motion:

d ~ + kx = 0. (3-9)

This has the solution

x = Ae~ktld. (3-10)

In order to determine the integration constant A approximately, we notice that the initial phase of the motion as described by (3-6)-(3-8) takes place almost instantaneously for vanishing m. Therefore, it would appear to a slow observer as if at time t = 0+ the mass were suddenly displaced to xlnax and then released. Hence, the slow phase of the motion would approximately be described by (3-10) with A given by (3-8):

l_ —(kld)t de

We thus have arrived at two different approximate solutions. Integrating (3-6) with (3-2) and (3-3), we obtain

x ^ 2 [1 “ e~idlm)t], (3-12)

which is valid for small times and which will be called the inner solution and denoted by a superscript i. The approximation (3-11) valid for large times will be called the outer solution and denoted by superscript o. Thus

(3-13)

(3-14)

We shall now see how this basically intuitive method may be systema­tized to yield additional terms in a power series of an appropriate small dimensionless parameter. First, it is necessary to introduce dimensionless variables. A suitable set is

f = (3-15)

(3-16)

(3-24)

Obviously, this corresponds to the solution (3-10) for large times, the outer solution. The determination of the constant A% must wait for the moment.

The inner solution happens in a very short time. Therefore, in order to be able to study the solution with some resolution, we need to “magnify” the region of interest. This is achieved by stretching the independent variable. A suitable stretching is in the present example obtained by introducing for the inner solution x* = ж1 as a new independent variable

t = t*/e, (3-25)

which transforms the differential equation (3-17) and boundary conditions (3-18) and (3-19) into

(3-26)

(3-27) (3-28)

Expansion in e, keeping l fixed, now gives the following inner expansion:

Xі = £ xi(t)en, (3-29)

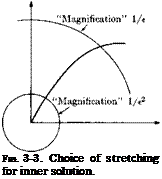
It is important to apply just the right amount of stretching in order to get a useful inner solution. In the present case we were guided by the physical insight into the problem which tells us that in the lowest-order term there should be a balance between inertia and damping terms, such as is retained in (3-30). If one applies too much stretching, for example, by setting instead of (3-25)

t = t*/e2, (3-32)

the features allowing one to match the inner and outer solutions (see below) would be lost. Thus with (3-32) the equation for the lowest-order term would be

j2 і

a xi

~dF

with the solution

Xі ~ et.

In other words, the “magnification ratio” is so large that only the initial linear portion of the solution can be kept in view. This is illustrated in Fig. 3-3. The amount of stretching necessary for each problem is usually evident from the physics of the prob­lem; however, a check on this will al­ways be whether the expansion works.

The solution of (3-30) satisfying the boundary conditions (3-27) and (3-28) is

4=1- e~l, (3-33)

which is equivalent to (3-12).

To complete the zeroth-order solution it remains to determine the constant Aq in (3-24). Let us assume that the validity of the inner and outer solutions overlaps in some region of t* and that in this region we
can find a t* = 5(e) such that we have

lira 5 = 0 (3-34)

£-►0

lim (5/e) = a). (3-35)

£—►0

Such a choice would be, for example, 5 = Ve. Requiring the two expan­sions to overlap in the limit gives (since the inner solution is expressed as a function of I = t*/e)

lim [4(«/e)J = Hm [4(5)] (3-36)

£->0 £—>0

or

4(co) = 4(0). (3-37)

This is termed the limit matching principle which in words may be stated as follows:

The outer limit of the inner expansion = the inner limit of the outer expansion.

From (3-33) it follows that

4(oo) = 4° = і

and from (3-24)

£o(0) = 4* = -do-

4° = 4*, A°0 = 1,

Applying the limit matching principle,

which leads to an outer solution identical to the previous one obtained through intuitive reasoning.

Notice that the formal approach is nothing but a formalization of the intuitive one. However, the formal approach is capable of being extended to give higher-order terms to any order in e, which the intuitive one is not. First, we may construct a composite solution that is uniformly valid to order e over the whole region by setting

С О I г oi

x0 ~ xQ + x0 — x0 .

It is seen that this solution, in view of the matching, approaches the inner and outer solutions in the inner and outer regions, respectively, and carries over smoothly in between them. In the problem considered, the zeroth- order composite solution becomes

_ e~l = e~e – e~fh.

To proceed to the next higher approximation it follows from (3-23) and (3-24), (3-39) that the next term in the outer expansion is a solution

°f, о

dx і о – Є

dr

which has the general solution

О — t* I AO—t*

X — —t 6 – p А.Є

The first-order inner solution must, according to (3-31) and (3-33), satisfy

(3-44)

The general solution of this equation is

x = A+ Be-{ – l – le~l (3-45)

The constants A and B are to be determined such that the inner bound­ary conditions (3-27) and (3-28) are fulfilled. Since the lowest-order term has already taken care of these, x and its first derivative must both be zero. This gives

А І = – В І = 2, (3-46)

and hence

x = 2(1 – e~l) – 1(1 + e~l). (3-47)

The two-term inner expansion is thus

Xі ~ x’o + ехІ = 1 – e~{ + «[2(1 – e~l) – <(1 + e~f)] (3-48)

or, expressed in the outer (physical) variable

Xі ~ 1 – t* – (1 + <*)<r’*/e + 2e(l – e~l*u). (3-49)

The two-term outer solution is obtained from (3-24) and (3-41) to be

x° ~ x°o + ехІ = e~l — et*e~( + eAie~‘ (3-50)

The behavior of this near the inner limit may be obtained by series expan­sion in t*. The first terms in such an expression are

xoi ~ 1 – t* – e(t* – AT). (3-51)

In the inner expansion, on the other hand, the exponential term will be negligible in the outer limit and thus

It is evident from comparison of (3-50) and (3-52) that the two expressions match if

A“ = 2. (3-53)

The procedure may be formalized as follows: Express the n-term inner expansion in outer variables and take the те-term outer expansion of this. In our case take n = m = 2. Then the two-term outer expansion of the two-term inner expansion as obtained from (3-49) is

xio ~ 1 – t* + 2e. (3-54)

Next, express the two-term outer expansion in inner variables. This gives

/ = e~li – e2Ie~tl + eA'[e;-d. ■ (3-55)

Take the two-term expansion of this. This yields

xoi ~ 1 – it + tAl. (3-56)

Reexpress this in outer variables. Hence

xoi ~ 1 – t* + 6At (3-57)

Equating (3-57) and (3-54) gives A'{ = 2 as before. We have shown an application of the asymptotic matching principle of Kaplun and Lagerstrom (1957) which may be stated as follows (Van Dyke, 1964):

The m-term outer expansion of (the n-term inner expansion) = the n-term inner expansion of {the m-term outer expansion).

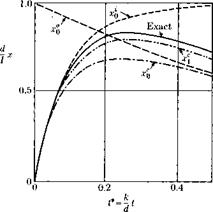
Fig. 3-4. Comparisons of various approximations for e = mk/d2 = 0.1.

This principle should hold for any combination of я and m, not only when they are equal as in the present case.

In the problems that will be treated in the following, mostly the limit matching principle will be used. We may now construct a composite expansion valid to first order by setting

жс ~ Xі + / – xio = (1 + 2e)(e~‘* – e~‘*le)

– + €c **). (3-58)

In Fig. 3-4 are shown the various approximate solutions for e = 0.1 together with the exact solution. As seen, the first-order composite solution gives a rather good approximation to the exact solution every­where, and the next term will probably account for practically all of the remaining difference.

We summarize now the main elements of the method:

(1) Writing the differential equations in a nondimensional form.

(2) Straightforward power series expansion of the differential equation and the associated boundary conditions using the physical variables. This gives the outer expansion.

(3) Suitable stretching of the independent variable to magnify the inner region sufficiently to be able to discern the details of the inner solution. Power series expansion of the solution in the small parameter keeping the stretched coordinate fixed gives the inner expansion.

(4) Matching the inner and outer expansions asymptotically.

(5) Constructing the composite expansion.

The method of matched asymptotic expansions has been used success­fully in a wide variety of fluid flow problems as well as in the theory of elasticity, and for some problems in rigid-body dynamics.

In the subsequent application of the method we will seldom proceed beyond the lowest-order approximation, in which case the limit matching principle usually suffices. Also composite expansions will only rarely be considered.