Expansive flow

There is, however, another way in which a supersonic flow can turn corners.

To understand this let us consider what happens at a convex corner, i. e. one at which, if the flow were to go straight on, it would get farther away from the surface (Fig. 12.6).

Figure 12.7 shows the result, though it must be admitted that it doesn’t really indicate the reason for what happens – this unfortunately can only be given in a mathematical treatment of the subject.

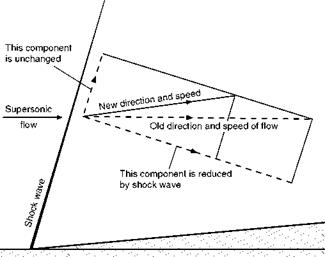
Fig 12.5 Change of direction and speed of flow

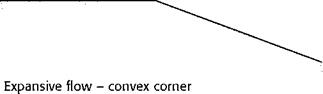Fig 12.6

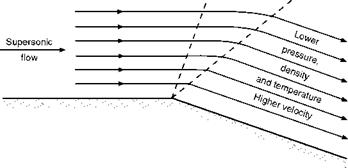
As we can see from the figures the supersonic airflow, on meeting a corner of this type, is free to expand; this it does, becoming more rarefied, i. e. decreasing in density in the decreased pressure, and the lines of flow are there­fore farther apart, and the temperature also falls as is usual in an expanding flow. The speed on the other hand increases.

So far it seems very similar to compressive flow – except that all the oppo­sites happen! There is, however, another fundamental difference which is illustrated on the figure though it may not be immediately obvious. The dotted lines indicate the slopes of the two Mach Tines, the first one for the velocity of flow before the corner, the second one after the corner; notice that the second one is at a more acute angle to the new surface than the first one is to the orig­inal surface, i. e. that the angle between the Mach Tines is greater than the change of angle of the surface – this of course is because the velocity after the corner is greater than before the corner. But more important than this is to notice that between the Mach Tines the flow changes gradually on a curved path, not suddenly as at a shock wave, because the Mach Tines no longer con­verge as in Fig. 12.2c, but, on the contrary, they now diverge.

This gradual change of flow helps to emphasise the fact that the Mach Tines are nothing like shock waves; for there is some danger that even the dotted lines in the figures may suggest that they are. If we go back to the original explanation of Mach Tines, it will be realised that, in comparison with shock waves, they are small weak waves that may appear anywhere along the surface, not just at corners, and that the flow passes through them without sudden changes in its direction or physical properties.

This type of flow is called expansive flow, and the phenomenon at the corner which causes the flow to change is sometimes called an expansion wave.

It should be noted that although the change at an expansion wave is gradual when compared with that at a shock wave, it still takes place over a very short time and distance compared with subsonic flow in which things happen long before – and long after – the corner is reached.

It should be noted, too, that although there is a limit to the angle through which supersonic flow can be turned at one expansion wave, it is possible to turn it through a large angle by a succession of expansion waves. In fact, of course a curved surface is an infinite series of corners, and over a convex curved surface there will be a succession of expansion waves, and the changes in direction of the flow, and in pressure, density, and temperature will be even more gradual, though still, unlike subsonic flow, being confined to the passage over the surface itself, and not before or after. So, although supersonic flow can turn sharp corners, it should not be thought that it cannot also be per­suaded to pass over curved surfaces, and this is a very good thing because even supersonic aeroplanes sometimes have to fly slowly and curved surfaces are very much better for low speeds.