Finite Control Volume Approach

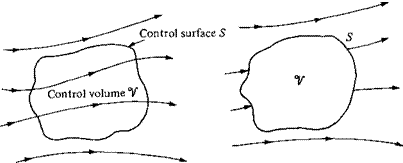
Consider a general flow field as represented by the streamlines in Figure 2.11. Let us imagine a closed volume drawn within a finite region of the flow. This volume defines a control volume V, and a control surface S is defined as the closed surface which bounds the control volume. The control volume may be fixed in space with the fluid moving through it, as shown at the left of Figure 2.11. Alternatively, the control volume may be moving with the fluid such that the same fluid particles are always inside it, as shown at the right of Figure 2.11. In either case, the control volume is a reasonably large, finite region of the flow. The fundamental physical principles are applied to the fluid inside the control volume, and to the fluid crossing the control surface (if the control volume is fixed in space). Therefore, instead of looking at the whole flow field at once, with the control volume model we limit our attention to just the fluid in the finite region of the volume itself.

2.3.1 Infinitesimal Fluid Element Approach

Consider a general flow field as represented by the streamlines in Figure 2.12. Let us imagine an infinitesimally small fluid element in the flow, with a differential volume dV. The fluid element is infinitesimal in the same sense as differential calculus; however, it is large enough to contain a huge number of molecules so that it can be viewed as a continuous medium. The fluid element may be fixed in space with the fluid moving through it, as shown at the left of Figure 2.12. Alternatively, it may be moving along a streamline with velocity V equal to the flow velocity at each point. Again, instead of looking at the whole flow field at once, the fundamental physical principles are applied to just the fluid element itself.

Figure 2.1 1 Finite control volume approach.

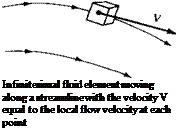Infinitesimal fluid element fixed in space with the fluid moving through it

Figure 2.12 Infinitesimal fluid element approach.