Flat-Plate Solution with a Polynomial Velocity Profile

For an example, we consider the flow over a flat plate and assume that the velocity profile is given by a third-order polynomial in n:

u = an3 + bn2 + cn + d. (8.105)

The constants in the equation can be evaluated using the boundary conditions that:

— = 0 at n = 0

—

= 1 at n = 1. V

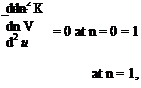These lead to the requirements that d = 0 and a + b + c = 1. For a flate plate, the external pressure gradient is zero, so this provides no additional information. To complete the evaluation of the coefficients, we require that derivatives of the velo­city profile at the freestream condition go to zero. This is consistent with an asymp­totic approach to the freestream. Thus, we write:

leading to the requirement that a = 1, b = -3, and c = 3. Therefore, a physically consis­tent polynomial for the flat-plate boundary-layer profile is:

—=n3 -3n2+3n.

The displacement thickness and momentum thicknesses divided by the boundary – layer thickness now can be found from their definitions:

-;r =j|1 – — dn = j (1- n3 + 3n2- 3n) dn = 0.25

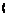
0

Hence, the two shape factors become:

– * -*/-

H = — = ^-^ = 2.333 0 0/-

H ‘ = – = 9.334.

0

The skin-friction coefficient also is given by:

du

dz

f~ 1

5* = 1.8704

To complete the calculation, the momentum-integral relationship, Eq. 8.103, is used to find the momentum thickness, 0. The momentum-integral relationship, with a zero pressure gradient, becomes: of the more popular of these in this subsection and leave a more thorough treat­ment for textbooks devoted more exclusively to the topic of boundary-layer theory.

5 *

The momentum-integral relationship can be written in terms of both the shape factor, H, and a shear factor, S. These are defined as follows:

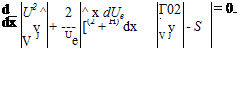When placed into the momentum-integral relationship we obtain:

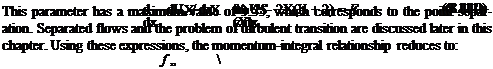Unfortunately, the previous approach assumed that the shear and shape factors were constant, which eliminates many potentially interesting flows from consider­ation. Instead, it is found that the factors H and S very nearly depend only on the quantity:

By analyzing a large volume of experimental and analytical results for laminar boundary layers in terms of these parameters, Thwaites proposed a simple linear relationship for F(X) given by:

F (X) = 0.45-6.0 X. (8.112)

02(*) v

0.45 Ue6(*)

92(*q) Ue6(x0) v Ue6(*)

This allows an immediate integration of the integral-momentum relationship as follows:

Note that once 02/v is found, the value of X can be computed. The shear and shape factors then can be computed from a table of H and S values as a function of X. Ana­lytic curve fits of these data are shown in (White, 1974), as follows:

H (X) = 2.0 + 4.14z – 83.5z2 + 854z3 + 3,337z4 + 4576z5 S(X) = (X + 0.09)0’62,

where the variable z in the H equation is defined as:

z = 0.25 – l.

These then can be used to determine the displacement thickness and the wall shear stress. A few examples demonstrate this simple but powerful method.

Constant-Speed Freestream over a Flat Plate

Here, Ue(x) = Uo, a constant, and the flow begins at the leading edge of the flat plate. In this case, the Thwaites integral becomes:

02 = 045x

v= U0 ,

which compares favorably with the exact (i. e., Blasius) value of 0.441x/Uo. We also note that here, X = 0 because the derivative of Ue is zero. Then, we find that:

H = 2.55 and 5 = 0.225.

These compare well with the exact values of H = 2.59 and S = 0.220. The skin friction on the plate is given by:

2vS

Ue0 ,

which now becomes:

This is within 1 percent of the exact result of 0.664 /VRX.