Fluid Statics: Buoyancy Force

In aerodynamics, we are concerned about fluids in motion, and the resulting forces and moments on bodies due to such motion. However, in this section, we consider the special case of no fluid motion, i. e., fluid statics. A body immersed in a fluid will still experience a force even if there is no relative motion between the body and the fluid. Let us see why.

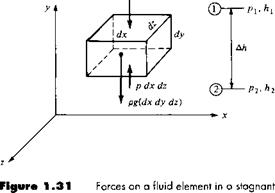
To begin, we must first consider the force on an element of fluid itself. Consider a stagnant fluid above the xz plane, as shown in Figure 1.31. The vertical direction is given by y. Consider an infinitesimally small fluid element with sides of length dx, dy, and dz. There are two types of forces acting on this fluid element: pressure forces from the surrounding fluid exerted on the surface of the element, and the gravity force due to the weight of the fluid inside the element. Consider forces in the у direction. The pressure on the bottom surface of the element is p, and hence the force on the bottom face is p(dx dz) in the upward direction, as shown in Figure

(p + ^dy)dx dz fluid.

1.31. The pressure on the top surface of the element will be slightly different from the pressure on the bottom because the top surface is at a different location in the fluid. Let dp/dy denote the rate of change of p with respect to y. Then the pressure exerted on the top surface will be p + (dp/dy) dy, and the pressure force on the top of the element will be [p + (dp/dy) dy](dx dz) in the downward direction, as shown in Figure 1.31. Hence, letting upward force be positive, we have

Net pressure force = p(dx dz) — ( p + —dy ) (dx dz)

dy J

= — — (dx dy dz) dy

Let p be the mean density of the fluid element. The total mass of the element is p(dx dy dz). Therefore,

Gravity force = —p(dx dy dz)g

where g is the acceleration of gravity. Since the fluid element is stationary (in equi­librium), the sum of the forces exerted on it must be zero:

-—(dx dy dz) – gp(dxdydz) = 0 dy

Equation (1.52) is called the Hydrostatic equation; it is a differential equation which relates the change in pressure dp in a fluid with a change in vertical height dy.

The net force on the element acts only in the vertical direction. The pressure forces on the front and back faces are equal and opposite and hence cancel; the same is true for the left and right faces. Also, the pressure forces shown in Figure 1.31 act at the center of the top and bottom faces, and the center of gravity is at the center of the elemental volume (assuming the fluid is homogeneous); hence, the forces in Figure 1.31 are colinear, and as a result, there is no moment on the element.

Equation (1.52) governs the variation of atmospheric properties as a function of altitude in the air above us. It is also used to estimate the properties of other planetary atmospheres such as for Venus, Mars, and Jupiter. The use of Equation (1.52) in the analysis and calculation of the “standard atmosphere” is given in detail in Reference 2; hence, it will not be repeated here.

Let the fluid be a liquid, for which we can assume p is constant. Consider points 1 and 2 separated by the vertical distance Ah as sketched on the right side of Figure

1.31. The pressure and у locations at these points are pi, h, and /?2, hi. respectively. Integrating Equation (1.52) between points 1 and 2, we have

Г P2 rhl

dp = – pg dy J p J h

Pi – Pi = ~Pg(hi — hj) — pg Ah

where Ah = h — hi. Equation (1.46) can be more conveniently expressed as

P2 + pgh2 = pi + pghi

Note that in Equations (1.53) and (1.54), increasing values of h are in the positive (upward) у direction.

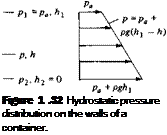
A simple application of Equation (1.54) is the calculation of the pressure distri­bution on the walls of a container holding a liquid, and open to the atmosphere at the top. This is illustrated in Figure 1.32, where the top of the liquid is at a heght hi. The atmospheric pressure pa is impressed on the top of the liquid; hence, the pressure at h is simply pa. Applying Equation (1.54) between the top (where h = h) and an arbitrary height h, we have

P + Pgh = pі + pghi = pa+ Pgh і

or p = Pa + pg(h – h) [1.55]

Equation (1.55) gives the pressure distribution on the vertical sidewall of the container as a function of h. Note that the pressure is a linear function of h as sketched on the right of Figure 1.32, and that p increases with depth below the surface.

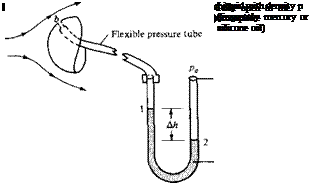
Another simple and very common application of Equation (1.54) is the liquid – filled U-tube manometer used for measuring pressure differences, as sketched in Figure 1.33. The manometer is usually made from hollow glass tubing bent in the shape of the letter U. Imagine that we have an aerodynamic body immersed in an airflow (such as in a wind tunnel), and we wish to use a manometer to measure the surface pressure at point b on the body. A small pressure orifice (hole) at point b is connected to one side of the manometer via a long (usually flexible) pressure tube. The other side of the manometer is open to the atmosphere, where the pressure pa is a known value. The U tube is partially filled with a liquid of known density p. The tops of the liquid on the left and right sides of the U tube are at points 1 and 2, with heights h and h2, respectively. The body surface pressure pt, is transmitted through the pressure tube and impressed on the top of the liquid at point 1. The atmospheric pressure pa is impressed on the top of the liquid at point 2. Because in general рь ф pa, the tops of the liquid will be at different heights; i. e., the two sides of the manometer will show a displacement Ah = hi — h2 of the fluid. We wish to

The use of a U-tube manometer.

obtain the value of the surface pressure at point b on the body by reading the value of Ah from the manometer. From Equation (1.54) applied between points 1 and 2,

Pb + pghi = pa + pgh2

or Pb = Pa – pg{h – h2)

or pb = Pa – pg Ah [1.56]

In Equation (1.56), pa, p, and g are known, and Ah is read from the U tube, thus allowing рь to be measured.

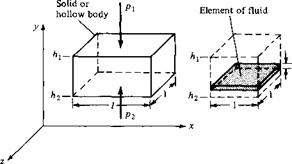
At the beginning of this section, we stated that a solid body immersed in a fluid will experience a force even if there is no relative motion between the body and the fluid. We are now in a position to derive an expression for this force, henceforth called the buoyancy force. We will consider a body immersed in either a stagnant gas or liquid, hence p can be a variable. For simplicity, consider a rectangular body of unit width, length/, and height {h—h2), as shown in Figure 1.34. Examining Figure 1.34, we see that the vertical force F on the body due to the pressure distribution over the surface is

F = (p2~ pi)l(l) [1.57]

There is no horizontal force because the pressure distributions over the vertical faces of the rectangular body lead to equal and opposite forces which cancel each other. In Equation (1.57), an expression for p2 — p can be obtained by integrating the hydrostatic equation, Equation (1.52), between the top and bottom faces:

ГР2 phi ph

P2 ~ Pi = dp = — I pgdy = I

J pi J h і «/ hi

Figure 1.34 Source of the buoyancy force on a body immersed in a fluid.

Substituting this result into Equation (1.57), we obtain for the buoyancy force

h

pgdy [1.58]

2

Consider the physical meaning of the integral in Equation (1.58). The weight of a small element of fluid of height dy and width and length of unity as shown at the right of Figure 1.34 is pg dy (1)(1). In turn, the weight of a column of fluid with a base of unit area and a height (h — /12) is

which is precisely the integral in Equation (1.58). Moreover, if we place l of these fluid columns side by side, we would have a volume of fluid equal to the volume of the body on the left of Figure 1.34, and the weight of this total volume of fluid would be

l pgdy J /12

which is precisely the right-hand side of Equation (1.58). Therefore, Equation (1.58) states in words that

Buoyancy force	weight of fluid
on body	— displaced by body

We have just proved the well-known Archimedes principle, first advanced by the Greek scientist, Archimedes of Syracuse (287-212 B. C.). Although we have used a rectangular body to simplify our derivation, the Archimedes principle holds for bodies of any general shape. (See Problem 1.14 at the end of this chapter.) Also, note from our derivation that the Archimedes principle holds for both gases and liquids and does not require that the density be constant.

The density of liquids is usually several orders of magnitude larger than the density of gases; e. g., for water p = 103 kg/m3, whereas for air p = 1.23 kg/m3. Therefore, a given body will experience a buoyancy force a thousand times greater in water than in air. Obviously, for naval vehicles buoyancy force is all important, whereas for airplanes it is negligible. On the other hand, lighter-than-air vehicles, such as blimps and hot-air balloons, rely on buoyancy force for sustenation; they obtain sufficient buoyancy force simply by displacing huge volumes of air. For most problems in aerodynamics, however, buoyancy force is so small that it can be readily neglected.

A hot-air balloon with an inflated diameter of 30 ft is carrying a weight of 800 lb, which includes the weight of the hot air inside the balloon. Calculate (a) its upward acceleration at sea level the instant the restraining ropes are released and (b) the maximum altitude it can achieve. Assume that the variation of density in the standard atmosphere is given by p = 0.002377(1 — 7 x 10~6/t)4-21, where h is the altitude in feet and p is in slug/ft3.

Solution

(a) At sea level, where h = 0, p = 0.002377 slug/ft3. The volume of the inflated balloon is |я(15)3 = 14,137 ft3. Hence,

Buoyancy force = weight of displaced air

= gpV

where g is the acceleration of gravity and V is the volume.

Buoyancy force = В = (32.2)(0.002377)(14,137) = 1082 lb

The net upward force at sea level is F = В — W, where W is the weight. From Newton’s second law,

F = В — W = та

where m is the mass, m = Щ = 24.8 slug. Hence,

_ B-W 1082 – 800 a ~ m ~ 24Я

(b) The maximum altitude occurs when В = W = 800 lb. Since В = gpV, and assuming the balloon volume does not change,

From the given variation of p with altitude, h,

p = 0.002377(1 – 7 x 10~6/t)4-21 = 0.00176

Solving for h, we obtain

1	0.00176 1/4 21
h =————	1 – (————-	—	9842 ft
7 x 10~6	V 0.002377 j