Fundamental Equations in Terms of the Substantial Derivative

In this section, we express the continuity, momentum, and energy equations in terms of the substantial derivative. In the process, we make use of the following vector identity:

v. (pV) =pV-V + V-Vp [2.106]

In words, this identity states that the divergence of a scalar times a vector is equal to the scalar times the divergence of the vector plus the dot product of the vector and the gradient of the scalar.

First, consider the continuity equation given in the form of Equation (2.52):

^ + V • (pV) = 0 [2.52]

ot

Using the vector identity given by Equation (2.106), Equation (2.52) becomes

— +V-Vp + pV-V = 0 [2.107]

31

However, the sum of the first two terms of Equation (2.107) is the substantial derivative of p [see Equation (2.104)]. Thus, from Equation (2.107),

Equation (2.108) is the form of the continuity equation written in terms of the sub­stantial derivative.

Next, consider the x component of the momentum equation given in the form of Equation (2.70a):

[2.70a]

The first terms can be expanded as

d{pu) dt

[2.109]

In the second term of Equation (2.70a), treat the scalar quantity as и and the vector quantity as pV. Then the term can be expanded using the vector identity in Equation (2.106):

V • (puV) = V • [a(pV)] = mV • (pV) + (pV)) • Vm [2.1 lO]

Substituting Equations (2.109) and (2.110) into (2.70a), we obtain

or

+ (pV) • Vm = – —- + pfx + (Fx) viscous [2.1 11] dx

Examine the two terms inside the square brackets; they are precisely the left side of the continuity equation, Equation (2.52). Since the right side of Equation (2.52) is zero, the sum inside the square brackets is zero. Hence, Equation (2.11) becomes

Эм dp _

P~—b pV • Vm = — ——- — h pfx + (Fx(viscous

dt dx

/Эм dp

or P ( — +V • VmJ =-—+ pfx + (^(viscous [2.112]

Examine the two terms inside the parentheses in Equation (2.12); their sum is precisely the substantial derivative Du/Dt. Hence, Equation (2.12) becomes

Du P~Dt ~

In a similar manner, Equations (2.10b and c) yield

[2.113b]

[2.113c]

Equations (2.113a to c) are the x, y, and z components of the momentum equation written in terms of the substantial derivative. Compare these equations with Equations (2.70a to c). Note that the right sides of both sets of equations are unchanged; only the left sides are different.

In an analogous fashion, the energy equation given in the form of Equation

(2.96) can be expressed in terms of the substantial derivative. The derivation is left as a homework problem; the result is

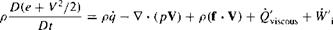[2.114]

Again, the right-hand sides of Equations (2.96) and (2.114) are the same; only the form of the left sides is different.

In modem aerodynamics, it is conventional to call the form of Equations (2.52), (2.70a to c), and (2.96) the conservation form of the fundamental equations (some­times these equations are labeled as the divergence form because of the divergence terms on the left side). In contrast, the form of Equations (2.108), (2.113a to c), and (2.114), which deals with the substantial derivative on the left side, is called the nonconservation form. Both forms are equally valid statements of the fundamental principles, and in most cases, there is no particular reason to choose one form over the other. The nonconservation form is frequently found in textbooks and in aerodynamic theory. However, for the numerical solution of some aerodynamic problems, the con­servation form sometimes leads to more accurate results. Hence, the distinction between the conservation form and the nonconservation form has become important in the modem discipline of computational fluid dynamics. (See Reference 7 for more details.)