Glauert’s and Later Nondimensional Forms
Hermann Glauert’scontribution to the evolution of the equationsof airplane motion was to introduce a dimensionless system based on the time unit т = p 1/V. In the expression for т, p is the airplane relative density m/pS1, and p is the air density. 1 and S are the airplane’s characteristic length and area, respectively. Typically 1 is the wing span and Sthe wing area. V is the airspeed. The relative density p is the ratio of airplane mass to the mass of air contained in a volume S x 1, determined by airplane size. Under Glauert’s system, time solutions come out in units of т seconds.
When the Glauert process is carried out, the numerical values of all symbols that appear in the equations (except for pi) depend only on the airplane’s shape, mass distribution, attitude, and angles of attack and sideslip. Airplane size, velocity, mass, and the air density, or altitude of flight, are all represented by the single parameter p.
Glauert defined new boldfaced dimensionless symbols such as t, w, q for time, vertical velocity, and pitching velocity, and k with an appropriate subscript for moment of inertia divided by 12 times m. The stability derivatives are likewise nondimensionalized. For example, xw stands for (dX/dw)/pVS. As B. Melvill Jones (1934) says:
When it is desired to convert the solutions so as to apply to a specified flight of a specified aeroplane in terms of specified units, it is merely necessary to multiply u, v, w, by V/p; p, q, r, by V/p1, and t by т (or m /pVS); where p, V, 1, S relate to the specified flight and are expressed in terms of the specified units.
If this is confusing to the reader, it was also confusing to the generation of stability and control engineers who practiced their art before electronic analog and then digital computers transformed the picture. Airplane time history calculations are now easy to make, so that there is no longer a premium on allowing a single dimensionless computation to represent many altitude, velocity (but not Mach number), size, and mass cases.
|
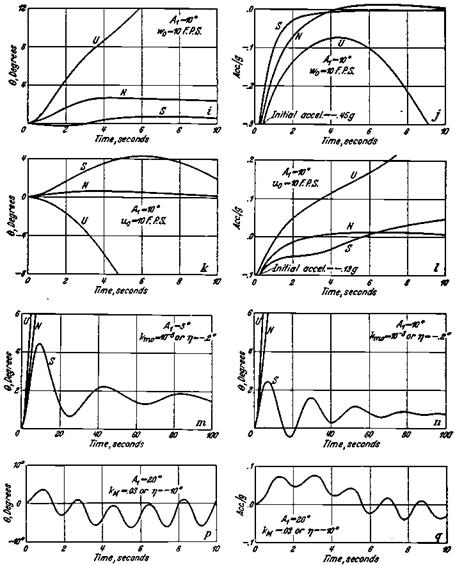
Figure 18.5 Examples of equation of motion solutions forthe Bristol F.2b (Bristol Fighter) produced in the 1930s for B. Melvill Jones’ section in Durand’s Aerodynamic Theory. The pitch attitude and normal acceleration solutions are for initial airspeed and vertical velocity perturbations and step elevator angles, at different equilibrium angles. |
Aerodynamic data are generated in dimensionless form as the computed output of wind – tunnel tests and are so presented to the engineers that use equations of airplane motion. However, the special time unit т has all but disappeared from the scene. Airplane motions are calculated in terms of actual, rather than dimensionless, velocity units, except for the angles of attack and sideslip. In Glauert’s day dimensionless aerodynamic coefficients in Britain were based on pV2, not (p/2)V2. Thus, Glauert’s dimensionless stability derivatives were half as big as NACA dimensionless stability derivatives, except for the pitching moment rate derivatives mw and mq, based on the time to fly a chord, not a half-chord.
It is hard to avoid the impression that Glauert’s ingenious nondimensional form of the equations of airplane motion put the dynamic stability and control field on a side track that ultimately led nowhere. This particular contribution of the brilliant Hermann Glauert was undone by the digital computer.
Special notation for the equations of airplane motion actually started before Glauert (see Bryant and Gates, 1937). Notation for the equations of airplane motion remains an interest in Britain, the country where it all began. As part of its “Engineering Sciences Data” series, the Royal Aeronautical Society issued in 1967 a review of airplane dynamics notation and a recommended new set of standards. This work built on an impressive five-part RAE Technical Report (Hopkin, 1966). Hopkin’s point of view is
Notation is an extension of language, and a Tower of Babel should not be allowed to grow.
By the time of Hopkin’s work, the growth in applications of the equations of airplane motion had produced a great number of possible notational methods. In order to accommodate them all without ambiguity, Hopkin was obliged to use unusual symbols, such as little half-moons over symbols. These seem not to have caught on, at least in the United States. Authors apparently are content to define symbols that are clear enough in the context of their work.
A dimensional form of the stability derivatives has become popular especially for linearized analysis, in which the derivatives are divided by either airplane mass or a moment of inertia function. This form provides airplane state vectors that are physically measurable, such as velocities and angular velocities. In this system the derivative Zu stands for (dZ/дu)/m, for example. This particular form of the stability derivatives is found in the reports of the influential Systems Technology, Inc., group.