Gliding

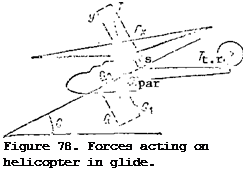
Rectilinear flight of the helicopter along an inclined trajectory with

the main rotor operating in the autorotative regime is termed gliding

(Figure 78). In this flight regime the helicopter is subject to the forces:

helicopter weight G, main rotor thrust T, parasite drag X, and tail rotor

p er

thrust T.

t. r

We resolve the helicopter weight force into two components: directed

along the flight trajectory, and G^ perpendicular to the trajectory.

We resolve the main rotor thrust force into the lift force Y and the drag force P.

The steady-state gliding condi­tions will be expressed by the equalities:

Y = G^ = G cos 0;

= X + P = G sin 0; par x

T = S ;
t. r s

V M = 0,

c. g

The first condition ensures constant gliding angle and rectilinear flight; the second assures constant speed along the trajectory. The tail rotor thrust is directed in the opposite direction in comparison with the thrust in the descent regime with the engine operating. The velocity along the trajectory and the gliding angle can be altered by tilting the thrust

force vector forward or aft, and also by varying the main rotor pitch. But we recall that flight takes place in the autorotative regime, and therefore the /127 pitch can be altered only within the permissible rpm limits. The pitch cannot be increased markedly, since the rotor may transition into the decelerated auto­rotation regime, and the rpm may become less than the minimal permissible value.

The main rotor autorotation conditions in a glide are much more complex than in a vertical descent. This is basically the result of two factors: azimuthal variation of the flow velocity over each blade element and the presence of blade falpping motions caused by transverse flow over the main rotor.

In a vertical descent each blade element has a constant velocity

In a glide this velocity depends on the blade azimuth and

changes continuously. In a vertical descent we can assume the absence of flapping motions, which simplifies the analysis of the blade element auto­rotative conditions. The flapping motions must be considered in a glide. But the derivations of the autorotation conditions which were carried out for the vertical descent remain valid for the gliding conditions as well. Let us recall these conclusions.

The autorotation conditions depend on the blade element pitch and the pitch of the entire main rotor: the lower the pitch, the greater the forward

tilt of the force vector AR and the higher the main rotor rpm.

The larger the angle of attack increment caused by the vertical descent velocity, the larger the forward tilt of the force vector AR and the higher the main rotor rpm.

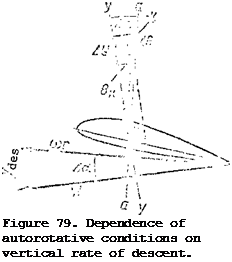
The latter conclusion is particularly important in clarifying the autoro­tation conditions in a glide, therefore, we shall examine the diagram in Figure 79. We see from the figure that the angle Да is equal to the angle between the lines y-y and a-a (y-y is perpendicular to the resultant velocity vector, a-a is perpendicular to the plane of rotation, or parallel to the hub rotation axis). Consequently, if Да>0 , the force vector AR will be tilted forward relative to the hub axis by the angle – y, and the rotor autorotation will be accelerated. The larger Да, the higher the main rotor rpm.

Keeping this analysis in mind, we turn to examination of the auto­rotation characteristics in a glide.

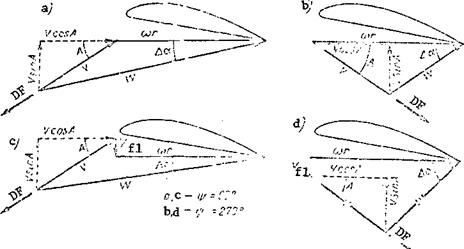
We first examine the influence on the autorotation conditions of the azimu­thal variation of the resultant blade element velocity. Since the resultant velocity varies continuously in azimuth we cannot analyze this variation directly. Therefore, we take the two most characteristic azimuths, 90 and 270°, and we compare the autorotation conditions at these azimuths (Figure 80). The flight direction along the trajectory is shown in the figure by the arrow DF. The main rotor hub rotation plane is horizontal, the angle of attack of the main rotor lies

between this plane and the gliding velocity vector and equals the gliding angle A = 0. At the 90° azimuth in the hub rotation plane, the flow approaches the blade element with the velocity г.’1–!- У ros 0 (Figure 80a). The blade ele­ment angle of attack increment caused by the vertical descent velocity can be found from the formula

V. sin 0

gl _______

шг + V, cos 0
gl

At the 270° azimuth the blade travels aft relative to the direction of flight, therefore, the flow approaches the blade element in the hub rotation plane with the velocity шг – V ^ cos 0 (Figure 80b). In this case, the angle of attack increment is

V sin 0

_Jgl__________

шг – V, cos 0
gl

Figure 80. Dependence of autorotative conditions on azimuth and flapping motions:

a, c – ф = 90°; b, d – ip = 270°

Comparing diagrams a and b, and also Formulas (43) and (44), we conclude that the angle of attack increment at the 270° azimuth is larger than at the 90° azimuth. Consequently, as a result of the variation of the resultant velocity in the gliding regime, there is a change of the angle of attack increment and tilt of the resultant aerodynamic force: at the 90° azimuth

the tilt is aft; at the 270° azimuth the tilt is forward.

Now let us examine the influence of flapping motions on the autorotation conditions.

As the advancing blade flaps up, the angles a and Да decrease. At the 90° azimuth, where the upward vertical flapping velocity reaches its maximal value (Figure 80c), the angle of attack increment becomes minimal

V sin 0 – T gl fl

шг + V.. cos 0
gl

Therefore, the maximal aft tilt of the force vector AR and the maximal blade retarding moment occur at this azimuth. The maximal down vertical flapping velocity will occur at the 270° azimuth. Therefore, in accordance with the formula

V і sin 0 + Jf. gl fl

юг – V, cos 0
gl

the blade element has the largest angle of attack increment (Figure 80d). The maximal forward tilt of the elemental force and the maximal turning moment will occur at this azimuth.

Thus, we draw the following conclusion. During gliding, the autorotation conditions of each blade element and the entire blade as a whole vary during a single revolution of the rotor. The advancing blade creates a retarding moment, which reduces the rotor rpm. The maximal retarding moment is created at the ф = 90° azimuth. The retreating blade creates a turning moment whose maximal value occurs at the 270° azimuth, where the angle of attack increment Да becomes maximal. This means that during a glide, the blades alternately accelerate and retard the rotation, and on the whole, the main rotor operates under steady-state autorotation conditions. The rotor rpm is regulated by the pitch: the lower the pitch, the higher the rotor rpm.