Governing Equations for Inviscid, Compressible Flow
In Chapters 3 to 6, we studied inviscid, incompressible flow; recall that the primary dependent variables for such flows are p and V, and hence we need only two basic equations, namely, the continuity and momentum equations, to solve for these two unknowns. Indeed, the basic equations are combined to obtain Laplace’s equation and
Bernoulli’s equation, which are the primary tools used for the applications discussed in Chapters 3 to 6. Note that both p and T are assumed to be constant throughout such inviscid, incompressible flows. As a result, no additional governing equations are required; in particular, there is no need for the energy equation or energy concepts in general. Basically, incompressible flow obeys purely mechanical laws and does not require thermodynamic considerations.
In contrast, for compressible flow, p is variable and becomes an unknown. Hence, we need an additional governing equation—the energy equation—which in turn introduces internal energy e as an unknown. Since e is related to temperature, then T also becomes an important variable. Therefore, the primary dependent variables for the study of compressible flow are p, V, p, e, and T; to solve for these five variables, we need five governing equations. Let us examine this situation further.
To begin with, the flow of a compressible fluid is governed by the basic equations derived in Chapter 2. At this point in our discussion, it is most important for you to be familiar with these equations as well as their derivation. Therefore, before proceeding further, return to Chapter 2 and carefully review the basic ideas and relations contained therein. This is a serious study tip, and if you follow it, the material in our next seven chapters will flow much easier for you. In particular, review the integral and differential forms of the continuity equation (Section 2.4), the momentum equation (Section 2.5), and the energy equation (Section 2.7); indeed, pay particular attention to the energy equation because this is an important aspect which sets compressible flow apart from incompressible flow.
For convenience, some of the more important forms of the governing equations for an inviscid, compressible flow from Chapter 2 are repeated below:
Continuity: From Equation (2.48),
![]()
![]()
![]() [7.39]
[7.39]
From Equation (2.52),
![]() 77 + V • PV = 0
77 + V • PV = 0
at
Momentum: From Equation (2.64),
|
|
|
|
|
|
|
|
|
|
|
|
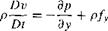
 |
Energy: From Equation (2.95),
In regard to the basic equations for compressible flow, please note that Bernoulli’s equation as derived in Section 3.2 and given by Equation (3.13) does not hold for compressible flow; it clearly contains the assumption of constant density, and hence is invalid for compressible flow. This warning is necessary because experience shows that a certain number of students of aerodynamics, apparently attracted by the simplicity of Bernoulli’s equation, attempt to use it for all situations, compressible as well as incompressible. Do not do it! Always remember that Bernoulli’s equation in the form of Equation (3.13) holds for incompressible flow only, and we must dismiss it from our thinking when dealing with compressible flow.
As a final note, we use both the integral and differential forms of the above equations in our subsequent discussions. Make certain that you feel comfortable with these equations before proceeding further.











