Helicopter Rate of Descent With Operating Engine
During inclined descent the helicopter speed along the trajectory and the
vertical rate of descent may vary from zero to the limiting permissible values.
In accordance with the second descent condition, the speed along the trajectory
will be constant if = X r + px* The flight speed can be altered by varying
the magnitude and direction of P. Since P depends on the position of the
X x
main rotor cone of rotation axis, there is a change of the helicopter speed along the trajectory when this position is changed. The helicopter motion velocity along the trajectory is connected with the vertical rate of descent as follows (Figure 70b)
|
|
|||
The vertical rate of descent is measured with the aid of a special instrument — a variometer. We see from the figure and Formula (38) that this rate depends on the velocity along the trajectory and the descent angle. The descent angle depends on the magnitude of the lift force Y, while the rate of descent depends on the force P, and therefore on the magnitude of the power supplied to the rotor. The helicopter rate of descent can be found from the Zhukovskiy grid.
If we draw on the Zhukovskiy grid, the lines showing power available N ; N
«X c*2»
for the given altitude, the points of their intersection with the
power required curves for the different regimes will correspond to definite
|
|
|
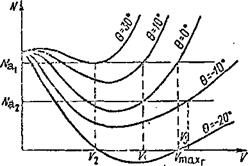

flight speeds along the trajectory. Thus, from the intersection of the line N& with the power required curves we can find the maximal helicopter horizontal flight velocity V, the vertical rate of climb V, for 0 = 10°, the ° max 1
vertical rate of climb V„ for 0 = 30°, and so on. Drawing the line N , we
L a2
find the vertical rate of descent for 0 ■ -10°. Other power available lines
must be drawn, i. e., lower engine powers must be used, to find the rates of
descent with larger descent angles.
The descent angles and velocities along the trajectory are often determined for some average altitude and some definite flight weight in the aerodynamic analysis. Such calculations are made for different values of main rotor pitch, for example, ф^; ; ф^. From the results of this calculation
we plot a graph — the polar curve of helicopter descent trajectories with operating engine (Figure 71b).
In this figure each curve corresponds to a definite velocity along the trajectory, if this velocity is plotted in the form of a vector from the coordinate origin. The horizontal axis will be the horizontal velocity
component V = V, cos 0, and the ordinate axis will be the vertical rate x des•t
of descent V, = V, ^ sin 0. The vertical rate of descent is measured in des des. t
m/sec, and the horizontal velocity is in km/hr. The velocity along the trajectory can be found if this velocity vector is transferred to the horizontal axis of the figure. Let us examine some characteristic points on the polar.
The point A lies at the intersection of the characteristic curve (for = 8°) with the ordinate axis. This point corresponds to helicopter vertical descent rate with the engine operating. If this rate of descent is more than 3 m/sec, transition to the vortex ring regime is possible and this cannot be permitted. This means that the pitch ф and the engine power must be increased.
The point В corresponds to descent with minimal permissible velocity along the trajectory, and the point C corresponds to descent with the minimal vertical rate of descent. In this case, the velocity along the trajectory corresponds to the economical velocity for horizontal flight of the helicopter.
The point D corresponds to flight with the minimal descent angle 0 , and in
this case, the velocity along the trajectory will be equal to the optimal helicopter horizontal flight speed.











