Helicopter Static Stability
General analysis of static stability. Static stability is the capability of the helicopter to restore disturbed equilibrium by itself after removal of the factors causing this disturbance. Static stability is attitude stability. The helicopter will be stable if after equilibrium is disrupted stabilizing moments develop on the helicopter, i. e., moments directed to restore the previous attitude. Static stability is amplified as a result of damping moments. A damping moment is one which is directed opposite the oscillatory motion of the helicopter about some axis. The difference between the stabilizing and damping moments is that the former arises as a result of equilibrium disruption and acts after the termination of this disruption. The damping moment acts only in the process of equilibrium disruption and is directed opposite the deviation.
If during and after equilibrium disruption, moments appear on the helicopter which deflect it still further from the previous attitude, such moments are termed destabilizing. The helicopter on which destabilizing moments arise is termed statically unstable. The helicopter on which no moments arise during and after the equilibrium disruption process has indifferent equilibrium and is termed statically neutral.
The factors which disturb equilibrium are:
(1) unsettled state of the air ("turbulence");
(2) random deflection of the control levers;
(3) failure of some part of the helicopter;
(4) change of the eg location.
Characteristic of helicopter equilibrium is the intimate interconnection of the individual equilibrium modes with one another. For example, if longitudinal equilibrium is disrupted, i. e., if the helicopter rotates about the transverse axis, the main rotor angle of attack changes. This involves a change of the thrust force and the reactive moment of the main rotor. The change of the reactive moment disrupts the directional equilibrium. Disruption of directional equilibrium leads to change of the tail rotor thrust force /160 and change of the moment of this force relative to the longitudinal axis, which means disruption of the helicopter transverse equilibrium. The intimate interconnection among the equilibrium modes requires constant action from the pilot, directed toward restoring the disrupted equilibrium, i. e., helicopter control becomes more complicated. Does the helicopter have static stability?
In order to answer this question we must examine the static stability of the main rotor, the static stability of the fuselage, and the effect of the stabilizer and tail rotor on the static stability.
Main rotor static stability with respect to velocity. When the helicopter equilibrium is disrupted, two motion parameters of the main rotor change: the flight velocity and the angle of attack. Let us assume that the helicopter is performing horizontal flight at the velocity V (Figure 98a). For some reason the flight velocity is increased by AV. As a result there is an increase of the flapping motions of the blades, the main rotor cone axis is deflected aft from the previous position, which is shown dashed in the figure, by the angle є. The tilt of the coning axis leads to the appearance of the force P, directed opposite the flight direction. Under the influence of this force the main rotor velocity will decrease.
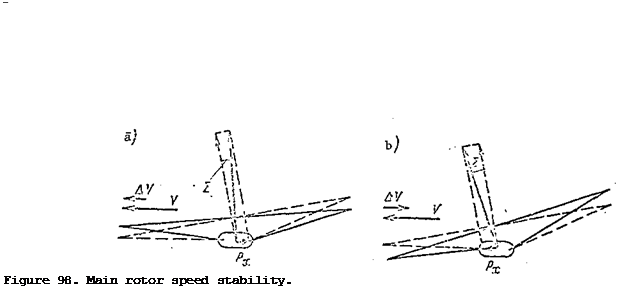
If the flight velocity is reduced by AV (Figure 98b), the cone axis is deflected forward, the force Px in the direction of flight develops, and the flight velocity will increase. The conclusion is that the main rotor has static stability with respect to velocity.
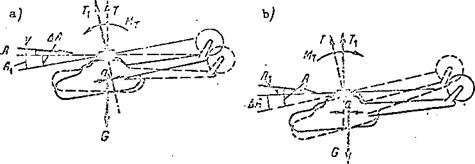
Main rotor static stability with respect to angle of attack. The helicopter is flying horizontally and the main rotor angle of attack is A. Under the influence of a vertical air current, the helicopter drops its nose and the main rotor angle of attack is reduced by AA (Figure 99a). Prior to disruption of equilibrium, the main rotor thrust force vector passed through the helicopter center of gravity and the moment of the thrust force was zero.
Upon disruption of the equilibrium, the thrust force vector T is deflected forward and the moment Mz = T^a develops relative to the helicopter transverse axis; this moment rotates the helicopter and the main rotor in the direction to reduce the angle of attack. Consequently, this moment will be destabilizing.
If for some reason the main rotor angle of attack is increased (Figure 99b), the thrust force vector tilts aft and a nose-up moment M^ = T^a is created, which causes the angle of attack to increase. A destabilizing thrust moment is created. The conclusion is that the main rotor is unstable with respect to angle of attack.
|
Figure 99. Main rotor angle-of-attack stability. |
Helicopter fuselage static stability. The fuselage has the second largest influence, after the main rotor, on the static stability of the helicopter.
The fuselage of the single-rotor helicopter has static instability about all three axes. A small stabilizer is installed at the aft end of the fuselage to improve longitudinal static stability in horizontal flight. In the hover regime and in flight at low velocity the stabilizer has practically no effect on longitudinal static stability. But with increase of the flight velocity and with reduction of the angle of attack, the longitudinal instability present in a hover decreases, and at negative angles of attack the fuselage plus stabilizer has longitudinal static stability. Thus, the fuselage of the Mi-1 has static stability at angles of attack from -10 to -2°. At positive angles of attack, the fuselage has indifferent longitudinal equilibrium.
The helicopter stabilizer is controllable. Stabilizer control is accomplished with the aid of the collective-throttle lever. When this lever is moved upward, main rotor pitch and stabilizer incidence angle are increased. The controllable stabilizer makes it possible to tilt the helicopter fuselage to a negative angle at the maximal slight speed. If the stabilizer angle were constant, a large negative lift force would develop on the stabilizer at a negative angle of attack, and this force would create a large nose-up moment to prevent tilting of the fuselage. When the rotor pitch is decreased the
stabilizer incidence angle becomes negative and a nose-up moment is developed, which aids in transitioning the main rotor into the autorotative regime. The main rotor angle of attack becomes positive, and as a result of the increase /162 of the angle of each blade element the rotor rpm increases.
The tail rotor also affects the fuselage static stability. The fuselage acquires directional stability as a result of the tail rotor. Thus, when directional equilibrium is disrupted, if the helicopter turns to the right for example (with right-hand rotation of the main rotor), the angles of attack of the tail rotor blade elements increase, and the tail rotor thrust force increases by ДТ. The moment of the tail rotor thrust also increases and equilibrium is restored.
If the helicopter turns to the right, the blade element angles of attack will decrease and therefore the thrust will decrease. The tail rotor moment becomes less than the main rotor reactive moment, and this leads to restoration of the equilibrium.
Since the tail rotor is mounted above the helicopter longitudinal axis and creates a transverse thrust moment, this leads to increase of the transverse static stability. Therefore, the tail rotor gives the fuselage directional and transverse static stability.
The conclusion is that the helicopter has slight static stability in horizontal flight and indifferent equilibrium in hover and in the other vertical flight regimes.
The static stability of twin-rotor helicopters differs somewhat from that of the single-rotor helicopter. The two-rotor helicopter with tandem arrangement of the rotors has considerably greater longitudinal static stability, while the two-rotor helicopter with side-by-side arrangement has higher transverse stability. This is explained by the variation of the thrust of the lifting rotors when equilibrium is disrupted.
Effect on helicopter static stability of horizontal hinge offset. If the main rotor huh has offset horizontal hinges, the horizontal hinge moments have considerable effect on the longitudinal and transverse static stability of the helicopter. The larger the horizontal hinge offset and the higher the main rotor rpm, the larger the main rotor damping moment and the greater the helicopter static stability. Thus, increase of the static stability is achieved by increasing the horizontal hinge offset. The appearance of the damping moment is explained by the gyroscopic properties of the main rotor.
As is well known, the basic property of the gyroscope is its ability to maintain the attitude of its axis of rotation fixed in space. This property shows up more strongly, the larger the mass and the higher the rpm of the rotating body. What effect does the gyroscopic effect of the main rotor have on the behavior of the helicopter? We shall use an example to investigat this question.
![]() Let us assume that the longitudinal equilibrium of the helicopter has been disturbed and it has started to rotate about the transverse axis in the nose-
Let us assume that the longitudinal equilibrium of the helicopter has been disturbed and it has started to rotate about the transverse axis in the nose-
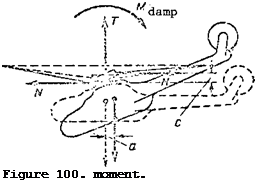 down direction (Figure 100). In view of its gyroscopic properties the main rotor will lag behind the helicopter rotation, therefore the main rotor hub axis is deflected from the cone-of – rotation axis. The horizontal hinge moment = Nc will be directed
down direction (Figure 100). In view of its gyroscopic properties the main rotor will lag behind the helicopter rotation, therefore the main rotor hub axis is deflected from the cone-of – rotation axis. The horizontal hinge moment = Nc will be directed
![]() opposite the tilt of the helicopter; therefore it will be a damping moment. When equilibrium is disrupted, the helicopter will rotate relative to the stationary cone-of-rotation axis of the main rotor as a result of the gyroscopic effect. And this means that the helicopter center of gravity will also displace together with the helicopter
opposite the tilt of the helicopter; therefore it will be a damping moment. When equilibrium is disrupted, the helicopter will rotate relative to the stationary cone-of-rotation axis of the main rotor as a result of the gyroscopic effect. And this means that the helicopter center of gravity will also displace together with the helicopter
|
relative to the cone-of-rotation axis (shown dashed in Figure 100). The result is the formation of the thrust moment = Та. The damping moment will be equal to the sum of the two moments + Hj, = Nc + Та. The
damping moment will be larger, the. higher the main rotor rpm, the larger the horizontal hinge offset, and the lower the position of the helicopter center of gravity, i. e., the larger the vertical eg displacement. The arm a and the thrust force moment will increase with increase of the distance Y from the hub rotation plane to the center of gravity.