Historical Note: The Illusive Center of Pressure

The center of pressure of an airfoil was an important matter during the development of aeronautics. It was recognized in the nineteenth century that, for a heavier-than – air machine to fly at stable, equilibrium conditions (e. g., straight-and-level flight), the moment about the vehicle’s center of gravity must be zero (see Chapter 7 of Reference 2). The wing lift acting at the center of pressure, which is generally a distance away from the center of gravity, contributes substantially to this moment. Hence, the understanding and prediction of the center of pressure was felt to be absolutely necessary in order to design a vehicle with proper equilibrium. On the other hand, the early experimenters had difficulty measuring the center of pressure, and much confusion reigned. Let us examine this matter further.

The first experiments to investigate the center of pressure of a lifting surface were conducted by the Englishman George Cayley (1773-1857) in 1808. Cayley was the inventor of the modem concept of the airplane, namely, a vehicle with fixed wings, a fuselage, and a tail. He was the first to separate conceptually the functions of lift and propulsion; prior to Cayley, much thought had gone into omithopters—machines that flapped their wings for both lift and thrust. Cayley rejected this idea, and in 1799, on a silver disk now in the collection of the Science Museum in London, he inscribed a sketch of a rudimentary airplane with all the basic elements we recognize

today. Cayley was an active, inventive, and long-lived man, who conducted numerous pioneering aerodynamic experiments and fervently believed that powered, heavier – than-air, manned flight was inevitable. (See Chapter 1 of Reference 2 for an extensive discussion of Cayley’s contributions to aeronautics.)

In 1808, Cayley reported on experiments of a winged model which he tested as a glider and as a kite. His comments on the center of pressure are as follows:

By an experiment made with a large kite formed of an hexagon with wings extended from it, all so constructed as to present a hollow curve to the current, I found that when loaded nearly to 1 lb to a foot and 1/2, it required the center of gravity to be suspended so as to leave the anterior and posterior portions of the surface in the ratio of 3 to 7. But as this included the tail operating with a double leverage behind, I think such hollow surfaces relieve about an equal pressure on each part, when they are divided in the ratio of 5 to 12, 5 being the anterior portion. It is really surprising to find so great a difference, and it obliges the center of gravity of flying machines to be much forwarder of the center of bulk (the centroid) than could be supposed a priori.

Here, Cayley is saying that the center of pressure is 5 units from the leading edge and 12 units from the trailing edge; i. e., xcp = 5/1 7c. Later, he states in addition: “I tried a small square sail in one plane, with the weight nearly the same, and I could not perceive that the center-of-resistance differed from the center of bulk.” That is, Cayley is stating that the center of pressure in this case is 1 /2c.

There is no indication from Cayley’s notes that he recognized that center of pressure moves when the lift, or angle of attack, is changed. However, there is no doubt that he was clearly concerned with the location of the center of pressure and its effect on aircraft stability.

The center of pressure on a flat surface inclined at a small angle to the flow was studied by Samuel R Langley during the period 1887-1896. Langley was the secretary of the Smithsonian at that time, and devoted virtually all his time and much of the Smithsonian’s resources to the advancement of powered flight. Langley was a highly respected physicist and astronomer, and he approached the problem of powered flight with the systematic and structured mind of a scientist. Using a whirling arm apparatus as well as scores of rubber-band powered models, he collected a large bulk of aerodynamic information with which he subsequently designed a full-scale aircraft. The efforts of Langley to build and fly a successful airplane resulted in two dismal failures in which his machine fell into the Potomac River—the last attempt being just 9 days before the Wright brothers’ historic first flight on December 17, 1903. In spite of these failures, the work of Langley helped in many ways to advance powered flight. (See Chapter 1 of Reference 2 for more details.)

Langley’s observations on the center of pressure for a flat surface inclined to the flow are found in the Langley Memoir on Mechanical Flight, Part I, 1887 to 1896, by Samuel P. Langley, and published by the Smithsonian Institution in 1911—5 years after Langley’s death. In this paper, Langley states:

The center-of-pressure in an advancing plane in soaring flight is always in advance of the center of figure, and moves forward as the angle-of-inclination of the sustaining

surfaces diminishes, and, to a less extent, as horizontal flight increases in velocity. These facts furnish the elementary ideas necessary in discussing the problem of equilibrium, whose solution is of the most vital importance to successful flight.

The solution would be comparatively simple if the position of the center-of- pressure could be accurately known beforehand, but how difficult the solution is may be realized from a consideration of one of the facts just stated, namely, that the position of the center-of – pressure in horizontal flight shifts with velocity of the flight itself.

Here, we see that Langley is fully aware that the center of pressure moves over a lifting surface, but that its location is hard to pin down. Also, he notes the correct variation for a flat plate, namely, xcp moves forward as the angle of attack decreases. However, he is puzzled by the behavior of xcp for a curved (cambered) airfoil. In his own words:

Later experiments conducted under my direction indicate that upon the curved sur­faces I employed, the center-of-pressure moves forward with an increase in the angle of elevation, and backward with a decrease, so that it may lie even behind the center of the surface. Since for some surfaces the center-of-pressure moves backward, and for others forward, it would seem that there might be some other surface for which it will be fixed.

Here, Langley is noting the totally opposite behavior of the travel of the center of pressure on a cambered airfoil in comparison to a flat surface, and is indicating ever so slightly some of his frustration in not being able to explain his results in a rational scientific way.

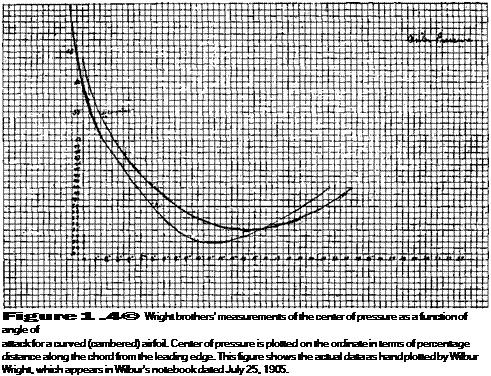
Three-hundred-fifty miles to the west of Langley, in Dayton, Ohio, Orville and Wilbur Wright were also experimenting with airfoils. As described in Section 1.1, the Wrights had constructed a small wind tunnel in their bicycle shop with which they conducted aerodynamic tests on hundreds of different airfoil and wing shapes during the fall, winter, and spring of 1901-1902. Clearly, the Wrights had an appreciation of the center of pressure, and their successful airfoil design used on the 1903 Wright Flyer is a testimonial to their mastery of the problem. Interestingly enough, in the written correspondence of the Wright brothers, only one set of results for the center of pressure can be found. This appears in Wilbur’s notebook, dated July 25, 1905, in the form of a table and a graph. The graph is shown in Figure 1.49—the original form as plotted by Wilbur. Here, the center of pressure, given in terms of the percentage of distance from the leading edge, is plotted versus angle of attack. The data for two airfoils are given, one with large curvature (maximum height to chord ratio = 1/12) and one with more moderate curvature (maximum height to chord ratio = 1/20). These results show the now familiar travel of the center of pressure for a curved airfoil, namely, xcp moves forward as the angle of attack is increased, at least for small to moderate values of a. However, the most forward excursion of xcp in Figure 1.49 is 33 percent behind the leading edge—the center of pressure is always behind the quarter-chord point.

The first practical airfoil theory, valid for thin airfoils, was developed by Ludwig Prandtl and his colleagues at Gottingen, Germany, during the period just prior to and

during World War I. This thin airfoil theory is described in detail in Chapter 4. The result for the center of pressure for a curved (cambered) airfoil is given by Equation

(4.66) , and shows that xcp moves forward as the angle of attack (hence q) increases, and that it is always behind the quarter-chord point for finite, positive values of q. This theory, in concert with more sophisticated wind-tunnel measurements that were being made during the period 1915-1925, finally brought the understanding and prediction of the location of the center of pressure for a cambered airfoil well into focus.

Because л:ср makes such a large excursion over the airfoil as the angle of attack is varied, its importance as a basic and practical airfoil property has diminished. Beginning in the early 1930s, the National Advisory Committee for Aeronautics (NACA), at its Langley Memorial Aeronautical Laboratory in Virginia, measured the properties of several systematically designed families of airfoils—airfoils which became a standard in aeronautical engineering. These NACA airfoils are discussed in Sections 4.2 and 4.3. Instead of giving the airfoil data in terms of lift, drag, and center of pressure, the NACA chose the alternate systems of reporting lift, drag, and moments about either the quarter-chord point or the aerodynamic center. These are totally appropriate alternative methods of defining the force-and-moment system on an airfoil, as discussed in Section 1.6 and illustrated in Figure 1.19. As a result, the

center of pressure is rarely given as part of modem airfoil data. On the other hand, for three-dimensional bodies, such as slender projectiles and missiles, the location of the center of pressure still remains an important quantity, and modem missile data frequently include xcp. Therefore, a consideration of center of pressure still retains its importance when viewed over the whole spectmm of flight vehicles.