Incompressible Flow over Airfoils
Of the many problems now engaging attention, the following are considered of immediate importance and will be considered by the committee as rapidly as funds can be secured for the purpose…. The evolution of more efficient wing sections of practical form, embodying suitable dimensions for an economical structure, with moderate travel of the center-of-pressure and still affording a large range of angle-of-attack combined with efficient action.
From the first Annual Report of the NACA, 1915
4,1 Introduction
With the advent of successful powered flight at the turn of the twentieth century, the importance of aerodynamics ballooned almost overnight. In turn, interest grew in the understanding of the aerodynamic action of such lifting surfaces as fixed wings on airplanes and, later, rotors on helicopters. In the period 1912-1918, the analysis of airplane wings took a giant step forward when Ludwig Prandtl and his colleagues at Gottingen, Germany, showed that the aerodynamic consideration of wings could be split into two parts: (1) the study of the section of a wing—an airfoil—and (2) the modification of such airfoil properties to account for the complete, finite wing. This approach is still used today; indeed, the theoretical calculation and experimental measurement of modem airfoil properties have been a major part of the aeronautics research carried out by the National Aeronautics and Space Administration (NASA) in the 1970s and 1980s. (See Chapter 5 of Reference 2 for a historical sketch on airfoil development and Reference 10 for a description of modem airfoil research.) Following Prandtl’s philosophy, the present chapter deals exclusively with airfoils,
|
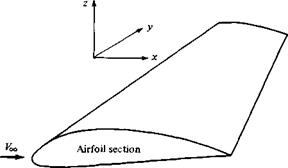
Figure 4.1 Definition of an airfoil. |
whereas Chapter 5 treats the case of a complete, finite wing. Therefore, in this chapter and Chapter 5, we make a major excursion into aerodynamics as applied to airplanes.
What is an airfoil? Consider a wing as drawn in perspective in Figure 4.1. The wing extends in the у direction (the span direction). The freestream velocity Voo is parallel to the xz plane. Any section of the wing cut by a plane parallel to the xz plane is called an airfoil. The purpose of this chapter is to present theoretical methods for the calculation of airfoil properties. Since we are dealing with inviscid flow, we are not able to predict airfoil drag; indeed, d’Alembert’s paradox says that the drag on an airfoil is zero—clearly not a realistic answer. We will have to wait until Chapter 15 and a discussion of viscous flow before predictions of drag can be made. However, the lift and moments on the airfoil are due mainly to the pressure distribution, which (below the stall) is dictated by inviscid flow. Therefore, this chapter concentrates on the theoretical prediction of airfoil lift and moments.
The road map for this chapter is given in Figure 4.2. After some initial discussion on airfoil nomenclature and characteristics, we present two approaches to low-speed airfoil theory. One is the classical thin airfoil theory developed during the period 1910-1920 (the right-hand branch of Figure 4.2). The other is the modem numerical approach for arbitrary airfoils using vortex panels (the left-hand branch of Figure 4.2). Please refer to this road map as you work your way through this chapter.