Influence of boundary layer type

In our description of the boundary layer, we explained how flow separation was influenced by whether the flow was laminar or turbulent. The importance of the type of boundary layer in the generation of boundary layer normal pres­sure (form) drag is well illustrated by the peculiar drag characteristics of com­ponents with a circular cross-section, such as undercarriage legs.

In Fig. 4.4 we show how the drag coefficient of a circular rod varies with speed. At low speeds, as at A, the boundary layer is laminar, and the separation points are well forward, as seen in Fig. 4.2. As the speed increases, a point is reached

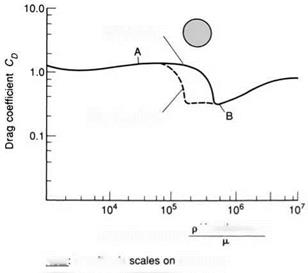Fig. 4.4 Some shapes show a dramatic variation in CD with Reynolds number

The value of CD at B is only about one quarter of the value at A. The drop is caused by a change in the nature of the boundary layer

where the boundary layer becomes turbulent before separation occurs. Because of the greater ability of the turbulent boundary layer to stay attached, the separa­tion positions move rearwards. The region of low pressure at the rear therefore narrows, and the drag coefficient is reduced sharply, as at position B in Fig. 4.4.

We thus have the rather surprising effect that, in this critical region, the change to a turbulent boundary layer results in a drop in drag coefficient! For the same basic reason, a similar erratic variation of drag coefficient with Reynolds number occurs on many shapes, including some aerofoil sections. This explains why wind tunnel test results taken at low Reynolds numbers can be misleading. If all of the experimental data were taken in the region to the left of A in Fig. 4.4, then one might have thought that the drag coefficient was more or less constant.

Because the transition to a turbulent boundary layer can cause a drop in the value of CD in the critical region, it is sometimes better to use a rough surface rather than a smooth one. The roughness provokes a turbulent boundary layer. It is for this reason that golf balls are given a dimpled surface. The reduction in drag coefficient enables the dimpled golf ball to fly further than a smooth one, for a given driving force.

As a turbulent boundary layer generates a greater surface friction drag than a laminar one, it is once again necessary to strike the correct balance between re­duction in boundary layer normal pressure drag, and rise in surface friction drag.

Note that roughening the surface will only have a beneficial effect if the Reynolds number is in the critical region. For the range of Reynolds numbers
used for aircraft flight, rough aerofoils nearly always have a higher drag coefficient than smooth ones. Exceptions to this rule sometimes occur on model aircraft, where the Reynolds numbers are so low, that laminar flow is likely to occur over most of the surface, with the probability of early flow separation. In this case, artificially turbulating the flow with patches of rough surface or trip wires, can sometimes reduce the drag coefficient.