Integral Conservation Theorems for Inviscid Fluid

For later use in connection with the calculation of forces and moments on wings and bodies, we wish to be able to express these quantities in terms of the fluxes of linear and angular momentum through arbitrary control surfaces S. This approach will often be found to have a special convenience, because singularities which occur in velocities and pressures at the surface of a vehicle may not persist at great distances in the flow field around it, so that the integrations which must be carried out are facilitated. The basic tools for carrying out this task are irftegrated forms of Newton’s law of motion known as momentum theorems.

In connection with the presentation of the momentum theorems, we take the opportunity to discuss the question of conservation of other flow properties, as expressed in integral form.

System boundary at a slightly later time

Q

Fixed control surface S and system boundar; at time t

Fig. 1-5. Control surface surroui___ 0 _ fluid volume and immersed body.

Immersed body surface a

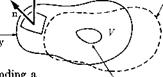
Consider any quantity E which is characteristic of the fluid particles contained within a fixed control volume V. Let V be bounded on the inside by one or more impermeable bodies, whose collective surfaces are denoted by the symbol a, and bounded on the outside by a larger fixed surface S. See Fig. 1-5. The closed system under examination is that fixed mass of fluid that happens to be contained within V at a certain instant of time. To find the rate of change of the total quantity for this system at the instant it coincides with V, we observe that this change is made up of the sum of all the local changes at points within V plus changes which occur as a result of the motion of the system boundary. Supposing that E is referred to unit volume of the fluid, the former rate of change can be

V

V

where the interchange of the operations of differentiation and integration is permissible in view of the constancy of the volume V. There is also an increment to the total amount of the quantity E as a result of the fact that the fluid is moving across the bounding surfaces S and a with a normal velocity component (Q • n). At points where this scalar product is positive, the fluid adjacent to an area element dS of the boundary takes up new positions outside this boundary, the volume per unit time passing outside the boundary being given by (Q • n) dS. Thus the rate of change of E for the system due to passage of fluid across the boundary is given by

<$E(Q ■ n) dS.

S+<r

Combining these last two results, we find for the total rate of change of this generalized property for the system,

= fffd-~dV + <£f>E(Q-n)dS. (1-44)

v s+o-

This general result is now specialized to several cases of interest.

1. Conservation of Mass or Continuity. To derive an integral continuity equation we replace E by the mass per unit volume p and observe that, in the absence of sources and sinks, the total mass of the system must remain constant. Thus we are led to

/// Ы dV + ^P(Q ‘ n) dS = °- (b45)

V S+cr

For steady flow around an impermeable body of fixed position, of course, the first integral in (1-45) vanishes, and the contribution to the second integral from the inner surface must be zero because the quantity in parentheses vanishes.

We note incidentally how from Gauss’ theorem, (1-14),

jfip(Q-n)dS = IJjv-(pQ)dV. (1-46)

S+tr V

Substituting into (1-45), we obtain

Since the volume V is arbitrary, the only way that this integral can vanish is for its integrand to be everywhere zero. Thus, the differential form of the continuity equation, (1-1), is confirmed.

2. Linear Momentum. Let F,- represent the vector sum of all forces applied by the surroundings to the system. According to Newton’s second law, this sum is equal to the time rate of change of linear momentum of the system, which corresponds to replacing E with the quantity pQ in (1—44). Consequently, we obtain the following generalized version of the law of conservation of momentum:

+ <ffpQ(Q ■ n) (IS. (1-48)

* V S+a

We now examine the various contributions that might appear to the force system in (1-48). If there is a conservative body force field, the left- hand side will include a quantity

jfjpFdV = JJJpVQ dV. (1-49)

v v

This will be omitted from what follows because of its relative unimportance in aeronautical applications.

The remaining external force will then be broken into two parts: the reaction (—Fbody) to the force exerted by the fluid on the body, and the force exerted across the outer boundary S by the surroundings. Recalling that n is the outward-directed normal, this latter might take the form

ffi—pn + r] dS,

5

where p is the pressure across S, and r is the sum of shear stress and devi – atoric normal stress exerted by the surroundings, if these are significant. We may write r as the dot product of a dyadic or tensor of deviatoric stress by the unit normal n. Since we are dealing generally with a non­viscous fluid, however, the question will not be elaborated here. Leaving out effects of shear stress, (1-48) can be modified to read

Again we remark that if the body is fixed in our coordinate system, the contribution to the second integral on the right from a will vanish. Also in steady flow the last term on the right is zero, leaving

Fbody = — <jij>lpn + pQ(Q ■ n)] dS. (1-51)

s

Equation (1-51) is actually the most useful form for practical applications. The specialized versions of (1-51) which occur when the flow involves
small perturbations will be discussed in a later chapter. It usually proves convenient to use an integrated form of the equations of motion (Ber­noulli’s equation) to replace the pressure in terms of the velocity field.

3. Angular Momentum. Let r be a vector of position measured from the origin about which moments are to be taken. Then it is an easy matter to derive the following counterpart of the first form of the linear momentum theorem:

Er*x F* = /// Jt(pr XQ)# + ^p(r X QKQ • n) dS- (1-52)

* V S+<7

The summation of moments on the left here can once more be broken up into a body-force term, a reaction to the moment exerted by the fluid through a and a pressure or shear moment exerted on the system over the outer boundary. Substitutions of this sort, neglecting the deviatoric stress, lead to the working form of the theorem of angular momentum:

Afbody = — ^ p(r X n) dS

s

S+a V

The steady-flow simplification involves dropping the integral over V and over the inner boundary a.

4. Thermodynamic Energy. Integral forms of the laws of thermo­dynamics will be found developed in detail in Chapter 2 of Shapiro (1953). Since these will have little direct usefulness in later applications and since many new definitions are involved, none of these results are reproduced here. Shapiro’s equation (2.20), for instance, provides an excellent working form of the first law. It is of interest that, when the pressure work exerted on the boundaries is included, the quantity E in the second or boundary term on the right of (1-44) is found to be

Here z is the distance vertically upward in a parallel gravity field, and h is the enthalpy per unit mass, which proves to be the effective thermo­dynamic energy in steady flow.

As a sidelight on the question of energy conservation we note that, in a constant-density fluid without body forces, the only way that energy can be stored is in kinetic form. Hence, a very convenient procedure for calculating drag, or fluid resistance, is to find the rate of addition of kinetic
energy to the fluid per unit time and to equate this to the work done by the drag. This represents a balance of mechanical rather than thermo­dynamic energy. When the fluid is compressible and there are still no dissipative mechanisms present, energy can be radiated away by compres­sion waves in an acoustic fashion. Therefore, the problem of computing drag from energy balance becomes a good deal more complicated.