Inviscid Versus Viscous Flow

A major facet of a gas or liquid is the ability of the molecules to move rather freely, as explained in Section 1.2. When the molecules move, even in a very random fashion, they obviously transport their mass, momentum, and energy from one location to another in the fluid. This transport on a molecular scale gives rise to the phenomena

of mass diffusion, viscosity (friction), and thermal conduction. Such “transport phe­nomena” will be discussed in detail in Chapter 15. For our purposes here, we need only to recognize that all real flows exhibit the effects of these transport phenomena; such flows are called viscous flows. In contrast, a flow that is assumed to involve no friction, thermal conduction, or diffusion is called an inviscidflow. Inviscid flows do not truly exist in nature; however, there are many practical aerodynamic flows (more than you would think) where the influence of transport phenomena is small, and we can model the flow as being inviscid. For this reason, more than 70 percent of this book (Chapters 3 to 14) deals with inviscid flows.

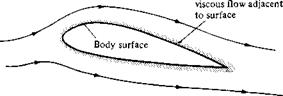
Theoretically, inviscid flow is approached in the limit as the Reynolds number goes to infinity (to be proved in Chapter 15). However, for practical problems, many flows with high but finite Re can be assumed to be inviscid. For such flows, the influence of friction, thermal conduction, and diffusion is limited to a very thin region adjacent to the body surface (the boundary layer, to be defined in Chapter 17), and the remainder of the flow outside this thin region is essentially inviscid. This division of the flow into two regions is illustrated in Figure 1.35. Hence, the material discussed in Chapters 3 to 14 applies to the flow outside the boundary layer. For flows over slender bodies, such as the airfoil sketched in Figure 1.35, inviscid theory adequately predicts the pressure distribution and lift on the body and gives a valid representation of the streamlines and flow field away from the body. However, because friction (shear stress) is a major source of aerodynamic drag, inviscid theories by themselves cannot adequately predict total drag.

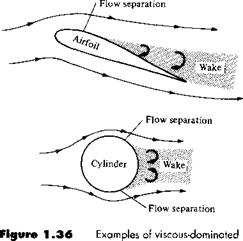
In contrast, there are some flows that are dominated by viscous effects. For example, if the airfoil in Figure 1.35 is inclined to a high incidence angle to the flow (high angle of attack), then the boundary layer will tend to separate from the top surface, and a large wake is formed downstream. The separated flow is sketched at the top of Figure 1.36; it is characteristic of the flow field over a “stalled” airfoil. Separated flow also dominates the aerodynamics of blunt bodies, such as the cylinder at the bottom of Figure 1.36. Here, the flow expands around the front face of the cylinder, but separates from the surface on the rear face, forming a rather fat wake downstream. The types of flow illustrated in Figure 1.36 are dominated by viscous

effects; no inviscid theory can independently predict the aerodynamics of such flows. They require the inclusion of viscous effects, to be presented in Part 4.