Kelvin’s Circulation Theorem and the Starting Vortex

In this section, we put the finishing touch to the overall philosophy of airfoil theory before developing the quantitative aspects of the theory itself in subsequent sections. This section also ties up a loose end introduced by the Kutta condition described in the previous section. Specifically, the Kutta condition states that the circulation around an airfoil is just the right value to ensure that the flow smoothly leaves the trailing edge. Question: How does nature generate this circulation? Does it come from nowhere, or is circulation somehow conserved over the whole flow field? Let us examine these matters more closely.

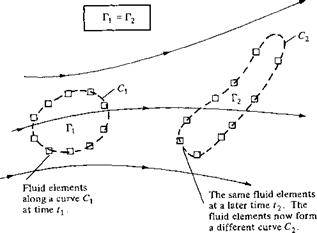
Consider an arbitrary inviscid, incompressible flow as sketched in Figure 4.15. Assume that all body forces f are zero. Choose an arbitrary curve C, and identify the fluid elements that are on this curve at a given instant in time t{. Also, by definition the circulation around curve Cj is Ті = — fc V • ds. Now let these specific fluid elements move downstream. At some later time, t2, these same fluid elements will form another curve C2, around which the circulation is Г2 = – fr У • ds. For the conditions stated above, we can readily show that Tt = Г2. In fact, since we are following a set of specific fluid elements, we can state that circulation around a closed curve formed by a set of contiguous fluid elements remains constant as the fluid elements move throughout the flow. Recall from Section 2.9 that the substantial derivative gives the time rate of change following a given fluid element. Hence, a mathematical statement of the above discussion is simply

[4.11]

which says that the time rate of change of circulation around a closed curve consisting of the same fluid elements is zero. Equation (4.11) along with its supporting discussion

is called Kelvin’s circulation theorem.[15] Its derivation from first principles is left as Problem 4.3. Also, recall our definition and discussion of a vortex sheet in Section 4.4. An interesting consequence of Kelvin’s circulation theorem is proof that a stream surface which is a vortex sheet at some instant in time remains a vortex sheet for all times.

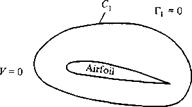
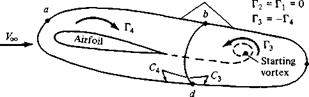
Kelvin’s theorem helps to explain the generation of circulation around an airfoil, as follows. Consider an airfoil in a fluid at rest, as shown in Figure 4.16a. Because V = 0 everywhere, the circulation around curve C is zero. Now start the flow in motion over the airfoil. Initially, the flow will tend to curl around the trailing edge, as explained in Section 4.5 and illustrated at the left of Figure 4.12. In so doing, the velocity at the trailing edge theoretically becomes infinite. In real life, the velocity tends toward a very large finite number. Consequently, during the very first moments after the flow is started, a thin region of very large velocity gradients (and therefore high vorticity) is formed at the trailing edge. This high-vorticity region is fixed to the same fluid elements, and consequently it is flushed downstream as the fluid elements begin to move downstream from the trailing edge. As it moves downstream, this thin sheet of intense vorticity is unstable, and it tends to roll up and form a picture similar to a point vortex. This vortex is called the starting vortex and is sketched in Figure 4.16b. After the flow around the airfoil has come to a steady state where the flow leaves the trailing edge smoothly (the Kutta condition), the high velocity gradients at the trailing edge disappear and vorticity is no longer produced at that point. However, the starting vortex has already been formed during the starting process, and it moves steadily downstream with the flow forever after. Figure 4.16b

shows the flow field sometime after steady flow has been achieved over the airfoil, with the starting vortex somewhere downstream. The fluid elements that initially made up curve C i in Figure 4.16a have moved downstream and now make up curve C2, which is the complete circuit abcda shown in Figure 4.16b. Thus, from Kelvin’s theorem, the circulation Г2 around curve C2 (which encloses both the airfoil and the starting vortex) is the same as that around curve C1, namely, zero. Г2 = F| = 0. Now let us subdivide C2 into two loops by making the cut bd, thus forming curves C3 (circuit bcdb) and C4 (circuit abda). Curve C3 encloses the starting vortex, and curve C4 encloses the airfoil. The circulation Г3 around curve C3 is due to the starting vortex; by inspecting Figure 4.16b, we see that Г3 is in the counterclockwise direction (i. e., a negative value). The circulation around curve C4 enclosing the airfoil is Г4. Since the cut bd is common to both C3 and C4, the sum of the circulations around C3 and C4 is simply equal to the circulation around C2:

r3 + Г4 = Г2

However, we have already established that Г2 = 0. Hence,

Г4 = – r3

that is, the circulation around the airfoil is equal and opposite to the circulation around the starting vortex.

This brings us to the summary as well as the crux of this section. As the flow over an airfoil is started, the large velocity gradients at the sharp trailing edge result in the

formation of a region of intense vorticity which rolls up downstream of the trailing edge, forming the starting vortex. This starting vortex has associated with it a coun­terclockwise circulation. Therefore, as an equal-and-opposite reaction, a clockwise circulation around the airfoil is generated. As the starting process continues, vorticity from the trailing edge is constantly fed into the starting vortex, making it stronger with a consequent larger counterclockwise circulation. In turn, the clockwise circu­lation around the airfoil becomes stronger, making the flow at the trailing edge more closely approach the Kutta condition, thus weakening the vorticity shed from the trailing edge. Finally, the starting vortex builds up to just the right strength such that the equal-and-opposite clockwise circulation around the airfoil leads to smooth flow from the trailing edge (the Kutta condition is exactly satisfied). When this happens, the vorticity shed from the trailing edge becomes zero, the starting vortex no longer grows in strength, and a steady circulation exists around the airfoil.