Laplace Transforms, Frequency Response, and Root Locus
One of the minor mysteries in the evolution of the equations of airplane motion is why it was not until 1950 that the Laplace transformation appeared in the open literature as a solution method for the airplane equations of motion. This was in an NACA Technical Note by Dr. G. A. Mokrzycki (1950), who later anglicized his name to G. A. Andrew. Laplace transforms were common among servomechanism engineers and in a few aeronautical offices for at least ten years before that. Laplace transforms provide a much simpler, more organized method for finding time history solutions than the classical operator methods described by B. Melvill Jones (1934) and Robert T. Jones (1936). Laplace transforms also provide a formal basis for airplane transfer functions, frequency responses, time vector analysis, and root loci, all used in the synthesis of stability augmentation systems, as described in Chapter 20, “Stability Augmentation.”
|
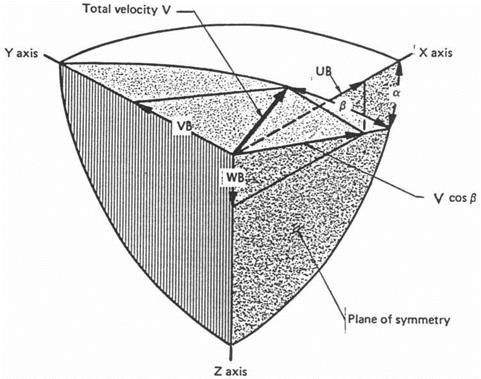
Figure 18.8 Usual angle-of-attack a and sideslip angle в convention, used in the NASA SIM2 flight simulation. X, Y, and Z are body axes. (From Abzug, Northrop paper, 1983) |