Large-eddy simulation
This approach to computational calculation of turbulent flow originated with meteorologists. In a sense LES is half way between the turbulence modelling based on Reynolds averaging and direct numerical simulations. LES is motivated by the view that the larger-scale motions are likely to vary profoundly between one type of turbulent flow and another, but that the small-scale turbulence is likely to be much more universal in character. Accordingly any semi-empirical turbulence modelling should be confined to the small-scale turbulence. With this in mind the flow variables are partitioned into
![]() {u, v, w, p] = {it, v, w, p} + {г/, і/, W, p’}
{u, v, w, p] = {it, v, w, p} + {г/, і/, W, p’}
4—- v—- ‘ 4—— V—- ‘
Resolved field Subgrid-scale field
The resolved or large-scale field is computed directly while the subgrid-scale field is modelled semi-empirically.
The resolved field is obtained by applying a filter to the flow variables, e. g.
![]() й(х) = J G(x-£) u(|)df
й(х) = J G(x-£) u(|)df
Filter function
If the filter function is chosen appropriately this has the effect of ‘averaging’ over the sub-grid scales.
Two common choices of filter function
|
I* — £l < Л/2 Otherwise |
(1) Box Filter*:
(2) Gaussian Filter
![]() G{x – Й = [0 ‘ ^-] exp [~b{x – g)1 /Ага
G{x – Й = [0 ‘ ^-] exp [~b{x – g)1 /Ага
The choice made for the size of A or Aa in Eqns (7.158) or (7.159) determines the sub-grid scale. Filtering the Navier-Stokes equations gives:
![]() дйі d ________ d _______ d ______ 1 dp 2 ~ . – _ –
дйі d ________ d _______ d ______ 1 dp 2 ~ . – _ –
-x – + -5— M«Mi + б-M<M2 + – s—м, м3= – + z/V М,- 1= 1,2,3
Ot OX 1 OX 2 OX 3 pOXj
 (7.161)
(7.161)
where щ, м2 and щ denote м, v and w, and леї, *2 and X3 denote x, у and z; and where
mj = ufij + u’fij + UyU[ + u’fij (7.162)
* Deardorff, J. W. (1970) A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers, J. Fluid Mech., 41, 453-480.
* Leonard, A. (1974) Energy cascade in large eddy simulations of turbulent fluid flow, Adv. Geophys., 18A, 237-248.
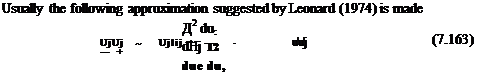 |
![]() modelled semi-empirically
modelled semi-empirically
Sub-grid scale modelling
A common approach, originating with Smagorinsky[53] is to use an eddy viscosity, so that
A common way of modelling sj is also due to Smagorinsky (1963):
![]() (7.165)
(7.165)
where c is a semi-empirically determined constant.
For more information on LES see Wilcox (1993) and Pope (2000). LES is very demanding in terms of computational resources but with the rapid increase in computer power it is becoming more and more feasible for engineering calculations. An alternative that is less demanding on computational resources is to use conventional turbulence modelling based on Reynolds averaging, but to include the time derivatives of the mean velocity components in the Reynolds-averaged Navier – Stokes equations. This approach is sometimes known as very-large-eddy simulation (VLES). See Tucker (2001)^ for a specialized treatment.











