. Lifting Flows over Arbitrary Bodies: The Vortex Panel Numerical Method

The thin airfoil theory described in Sections 4.7 and 4.8 is just what it says—it ap­plies only to thin airfoils at small angles of attack. (Make certain that you understand exactly where in the development of thin airfoil theory these assumptions are made and the reasons for making them.) The advantage of thin airfoil theory is that closed – form expressions are obtained for the aerodynamic coefficients. Moreover, the results compare favorably with experimental data for airfoils of about 12 percent thickness or less. However, the airfoils on many low-speed airplanes are thicker than 12 percent. Moreover, we are frequently interested in high angles of attack, such as occur during takeoff and landing. Finally, we are sometimes concerned with the generation of aerodynamic lift on other body shapes, such as automobiles or submarines. Hence, thin airfoil theory is quite restrictive when we consider the whole spectrum of aero­dynamic applications. We need a method that allows us to calculate the aerodynamic characteristics of bodies of arbitrary shape, thickness, and orientation. Such a method is described in this section. Specifically, we treat the vortex panel method, which is a numerical technique that has come into widespread use since the early 1970s. In reference to our road map in Figure 4.2, we now move to the left-hand branch. Also, since this chapter deals with airfoils, we limit our attention to two-dimensional bodies.

The vortex panel method is directly analogous to the source panel method de­scribed in Section 3.17. However, because a source has zero circulation, source panels are useful only for nonlifting cases. In contrast, vortices have circulation, and hence vortex panels can be used for lifting cases. (Because of the similarities between source and vortex panel methods, return to Section 3.17 and review the basic philosophy of the source panel method before proceeding further.)

The philosophy of covering a body surface with a vortex sheet of such a strength to make the surface a streamline of the flow was discussed in Section 4.4 We then went on to simplify this idea by placing the vortex sheet on the camber line of the airfoil as shown in Figure 4.11, thus establishing the basis for thin airfoil theory. We

now return to the original idea of wrapping the vortex sheet over the complete surface of the body, as shown in Figure 4.10. We wish to find у (s) such that the body surface becomes a streamline of the flow. There exists no closed-form analytical solution for y(s); rather, the solution must be obtained numerically. This is the purpose of the vortex panel method.

Let us approximate the vortex sheet shown in Figure 4.10 by a series of straight panels, as shown earlier in Figure 3.40. (In Chapter 3, Figure 3.40 was used to discuss source panels; here, we use the same sketch for discussion of vortex panels.) Let the vortex strength у (s) per unit length be constant over a given panel, but allow it to vary from one panel to the next. That is, for the n panels shown in Figure 3.40, the vortex panel strengths per unit length are y, y2,…, yj,…, y„. These panel strengths are unknowns; the main thrust of the panel technique is to solve for yj, j = 1 to n, such that the body surface becomes a streamline of the flow and such that the Kutta condition is satisfied. As explained in Section 3.17, the midpoint of each panel is a control point at which the boundary condition is applied; that is, at each control point, the normal component of the flow velocity is zero.

Let P be a point located at (x, y) in the flow, and let rpj be the distance from any point on the yth panel to P, as shown in Figure 3.40. The radius rpl makes the angle 0Pj with respect to the. r axis. The velocity potential induced at P due to the y’th panel, Дг/),, is, from Equation (4.3),

In Equation (4.72), yj is constant over the y’th panel, and the integral is taken over the jth panel only. The angle 6PJ is given by

[4.73]

In turn, the potential at P due to all the panels is Equation (4.72) summed over all the panels:

[4.74]

Since point P is just an arbitrary point in the flow, let us put P at the control point of the ith panel shown in Figure 3.40. The coordinates of this control point are (*,-, уi). Then Equations (4.73) and (4.74) become

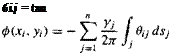-і Уі – Уі Xi-Xj

Equation (4.75) is physically the contribution of all the panels to the potential at the control point of the ith panel.

At the control points, the normal component of the velocity is zero; this velocity is the superposition of the uniform flow velocity and the velocity induced by all the vortex panels. The component of VA normal to the / th panel is given by Equation (3.148):

V0o. n = V0C cos p, [3.148]

The normal component of velocity induced at (a, , v, ) by the vortex panels is

v„ = [4.76]

an.

Combining Equations (4.75) and (4.76), we have

where the summation is over all the panels. The normal component of the flow velocity at the ith control point is the sum of that due to the freestream [Equation (3.148)] and that due to the vortex panels [Equation (4.77)]. The boundary condition states that this sum must be zero:

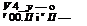
[4.78]

Substituting Equations (3.148) and (4.77) into (4.78), we obtain

[4.79]

Equation (4.79) is the crux of the vortex panel method. The values of the integrals in Equation (4.79) depend simply on the panel geometry; they are not properties of the flow. Let Jij be the value of this integral when the control point is on the ith panel. Then Equation (4.79) can be written as

П

Езо cos p, – ~ Ji. j = 0 [4.80]

i=і 171

Equation (4.80) is a linear algebraic equation with n unknowns, jq, Y2- ■ ■ ■■ Yn• It represents the flow boundary condition evaluated at the control point of the ith panel. If Equation (4.80) is applied to the control points of all the panels, we obtain a system of n linear equations with n unknowns.

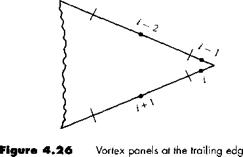
To this point, we have been deliberately paralleling the discussion of the source panel method given in Section 3.17; however, the similarity stops here. For the source panel method, the n equations for the n unknown source strengths are routinely solved, giving the flow over a nonlifting body. In contrast, for the lifting case with vortex panels, in addition to the n equations given by Equation (4.80) applied at all the panels, we must also satisfy the Kutta condition. This can be done in several ways. For example, consider Figure 4.26, which illustrates a detail of the vortex panel distribution at the trailing edge. Note that the length of each panel can be different; their length and distribution over the body are up to your discretion. Let the two panels at the trailing edge (panels і and і — 1 in Figure 4.26) be very small. The

Kutta condition is applied precisely at the trailing edge and is given by у (ТЕ) = 0. To approximate this numerically, if points і and г — 1 are close enough to the trailing edge, we can write

Yi = ~Yi- [4.81]

such that the strengths of the two vortex panels і and і — 1 exactly cancel at the point where they touch at the trailing edge. Thus, in order to impose the Kutta condition on the solution of the flow, Equation (4.81) (or an equivalent expression) must be included. Note that Equation (4.80) evaluated at all the panels and Equation (4.81) constitute an overdetermined system of n unknowns with n + 1 equations. Therefore, to obtain a determined system, Equation (4.80) is not evaluated at one of the control points on the body. That is, we choose to ignore one of the control points, and we evaluate Equation (4.80) at the other n — 1 control points. This, in combination with Equation (4.81), now gives a system of n linear algebraic equations with n unknowns, which can be solved by standard techniques.

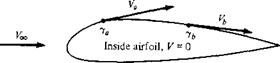
At this stage, we have conceptually obtained the values of y, y2,…, yn which make the body surface a streamline of the flow and which also satisfy the Kutta condition. In turn, the flow velocity tangent to the surface can be obtained directly from y. To see this more clearly, consider the airfoil shown in Figure 4.27. We are concerned only with the flow outside the airfoil and on its surface. Therefore, let the velocity be zero at every point inside the body, as shown in Figure 4.27. In particular, the velocity just inside the vortex sheet on the surface is zero. This corresponds to U2 = 0 in Equation (4.8). Hence, the velocity just outside the vortex sheet is, from Equation (4.8),

у = U — U2 = U — 0 = Ml

In Equation (4.8), и denotes the velocity tangential to the vortex sheet. In terms of the picture shown in Figure 4.27, we obtain Va = ya at point а, V/, = yh at point b, etc. Therefore, the local velocities tangential to the airfoil surface are equal to the local values of у. In turn, the local pressure distribution can be obtained from Bernoulli’s equation.

The total circulation and the resulting lift are obtained as follows. Let sj be the length of the yth panel. Then the circulation due to the у th panel is y, s r In turn, the

Figure 4.27 Airfoil as a solid body, with zero velocity inside the profile.

total circulation due to all the panels is

n

г = &л [4-821

./=1

Hence, the lift per unit span is obtained from

П

L’ = Poo Too y. isJ [4.83]

./=>

The presentation in this section is intended to give only the general flavor of the vortex panel method. There are many variations of the method in use today, and you are encouraged to read the modem literature, especially as it appears in the A/A4 Journal and the Journal of Aircraft since 1970. The vortex panel method as described in this section is termed a “first-order” method because it assumes a constant value of у over a given panel. Although the method may appear to be straightforward, its numerical implementation can sometimes be frustrating. For example, the results for a given body are sensitive to the number of panels used, their various sizes, and the way they are distributed over the body surface (i. e., it is usually advantageous to place a large number of small panels near the leading and trailing edges of an airfoil and a smaller number of larger panels in the middle). The need to ignore one of the control points in order to have a determined system in n equations for n unknowns also introduces some arbitrariness in the numerical solution. Which control point do you ignore? Different choices sometimes yield different numerical answers for the distribution of у over the surface. Moreover, the resulting numerical distributions for у are not always smooth, but rather, they have oscillations from one panel to the next as a result of numerical inaccuracies. The problems mentioned above are usually overcome in different ways by different groups who have developed relatively sophisticated panel programs for practical use. For example, what is more common today is to use a combination of both source and vortex panels (source panels to basically simulate the airfoil thickness and vortex panels to introduce circulation) in a panel solution. This combination helps to mitigate some of the practical numerical problems just discussed. Again, you are encouraged to consult the literature for more information.

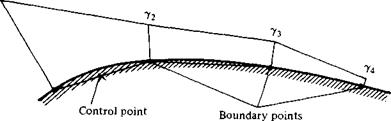
Such accuracy problems have also encouraged the development of higher-order panel techniques. For example, a “second-order” panel method assumes a linear variation of у over a given panel, as sketched in Figure 4.28. Here, the value of у at the edges of each panel is matched to its neighbors, and the values y, y2, уз, etc. at the boundary points become the unknowns to be solved. The flow-tangency boundary condition is still applied at the control point of each panel, as before. Some results using a second-order vortex panel technique are given in Figure 4.29, which shows

Figure 4.28 Linear distribution of у over each panel—a second-order panel method.

Figure 4.29 Pressure coefficient distribution over an NACA 0012 airfoil; comparison between second-order vortex panel method and NACA theoretical results from Reference 1 1. The numerical panel results were obtained by one of the author’s graduate students, Mr. Tae-Hwan Cho.

the distribution of pressure coefficients over the upper and lower surfaces of an NACA 0012 airfoil at a 9° angle of attack. The circles and squares are numerical results from a second-order vortex panel technique developed at the University of Maryland, and the solid lines are from NACA results given in Reference 11. Excellent agreement is obtained.

Again, you are encouraged to consult the literature before embarking on any serious panel solutions of your own. For example, Reference 14 is a classic paper on panel methods, and Reference 15 highlights many of the basic concepts of panel methods along with actual computer program statement listings for simple applica­tions. Reference 66 is a modern compilation of papers, several of which deal with current panel techniques. Finally, Katz and Plotkin (Reference 67) give perhaps the most thorough discussion of panel techniques and their foundations to date.