Line Integrals

Consider a vector field

A = A(x, y, z) = A(r, в, z) = A (г, в, Ф)

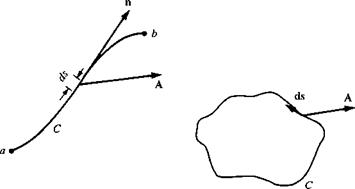
Also, consider a curve C in space connecting two points a and b as shown on the left side of Figure 2.8. Let ds be an elemental length of the curve, and n be a unit vector tangent to the curve. Define the vector ds = n ds. Then, the line integral of A along curve C from point a to point b is

A • ds

If the curve C is closed, as shown at the right of Figure 2.8, then the line integral is given by

J. A • ds

where the counterclockwise direction around C is considered positive. (The positive direction around a closed curve is, by convention, that direction you would move such that the area enclosed by C is always on your left.)