Molecular Approach

In actuality, of course, the motion of a fluid is a ramification of the mean motion of its atoms and molecules. Therefore, a third model of the flow can be a microscopic approach wherein the fundamental laws of nature are applied directly to the atoms and molecules, using suitable statistical averaging to define the resulting fluid properties. This approach is in the purview of kinetic theory, which is a very elegant method with many advantages in the long run. However, it is beyond the scope of the present book.

In summary, although many variations on the theme can be found in different texts for the derivation of the general equations of fluid flow, the flow model can usually be categorized under one of the approaches described above.

2.3.2 Physical Meaning of the Divergence of Velocity

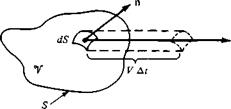
In the equations to follow, the divergence of velocity, V • V, occurs frequently. Before leaving this section, let us prove the statement made earlier (Section 2.2) that V • V is physically the time rate of change of the volume of a moving fluid element of fixed mass per unit volume of that element. Consider a control volume moving with the fluid (the case shown on the right of Figure 2.11). This control volume is always made up of the same fluid particles as it moves with the flow; hence, its mass is fixed, invariant with time. However, its volume V and control surface S are changing with time as it moves to different regions of the flow where different values of p exist. That is, this moving control volume of fixed mass is constantly increasing or decreasing its volume and is changing its shape, depending on the characteristics of the flow. This control volume is shown in Figure 2.13 at some instant in time. Consider an infinitesimal element of the surface d S moving at the local velocity V, as shown in Figure 2.13. The change in the volume of the control volume AV, due to just the

Figure 2.1 3 Moving control volume used for the physical interpretation of the divergence of velocity.

movement of dS over a time increment At, is, from Figure 2.13, equal to the volume of the long, thin cylinder with base area dS and altitude (V At) • n; i. e.,

ДУ = [(VAf) • n]dS = (VAt) ■ dS [2.28]

Over the time increment At, the total change in volume of the whole control volume is equal to the summation of Equation (2.28) over the total control surface. In the limit as dS —>■ 0, the sum becomes the surface integral

(VAt) • dS

If this integral is divided by At, the result is physically the time rate of change of the control volume, denoted by DV/Df, i. e.,

(The significance of the notation D/Dt is revealed in Section 2.9.) Applying the divergence theorem, Equation (2.26), to the right side of Equation (2.29), we have

^ – V)dV [2.30]

v

Now let us imagine that the moving control volume in Figure 2.13 is shrunk to a very small volume 8V, essentially becoming an infinitesimal moving fluid element as sketched on the right of Figure 2.12. Then Equation (2.30) can be written as

sv

Assume that 8 V is small enough such that V • V is essentially the same value through­out (5 V. Then the integral in Equation (2.31) can be approximated as (V • V)i5V. From

Equation (2.31), we have

= (V • V)5V

Examine Equation (2.32). It states that V • V is physically the time rate of change of the volume of a moving fluid element, per unit volume. Hence, the interpretation of V • V, first given in Section 2.2.6, Divergence of a Vector Field, is now proved.