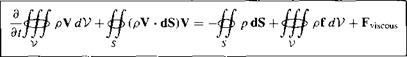Momentum Equation

Newton’s second law is frequently written as

F = та [2.55]

where F is the force exerted on a body of mass m and a is the acceleration. However, a more general form of Equation (2.55) is

F = — (mV) [2.56]

at

which reduces to Equation (2.55) for a body of constant mass. In Equation (2.56), mV is the momentum of a body of mass m. Equation (2.56) represents the second fundamental principle upon which theoretical fluid dynamics is based.

Physical principle Force = time rate of change of momentum

We will apply this principle [in the form of Equation (2.56)] to the model of a finite control volume fixed in space as sketched in Figure 2.17. Our objective is to obtain expressions for both the left and right sides of Equation (2.56) in terms of the familiar flow-field variables p, p, V, etc. First, let us concentrate on the left side of Equation

(2.56) , i. e., obtain an expression for F, which is the force exerted on the fluid as it flows through the control volume. This force comes from two sources:

1. Body forces: gravity, electromagnetic forces, or any other forces which “act at a distance” on the fluid inside V.

2. Surface forces: pressure and shear stress acting on the control surface S.

Let f represent the net body force per unit mass exerted on the fluid inside V. The body force on the elemental volume dV in Figure 2.17 is therefore

pi dV

and the total body force exerted on the fluid in the control volume is the summation of the above over the volume V:

where the negative sign indicates that the force is in the direction opposite of dS. That is, the control surface is experiencing a pressure force which is directed into the control volume and which is due to the pressure from the surroundings, and examination of Figure 2.17 shows that such an inward-directed force is in the direction opposite of
dS. The complete pressure force is the summation of the elemental forces over the entire control surface:

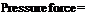
[3.58]

In a viscous flow, the shear and normal viscous stresses also exert a surface force. A detailed evaluation of these viscous stresses is not warranted at this stage of our discussion. Let us simply recognize this effect by letting Fuscous denote the total viscous force exerted on the control surface. We are now ready to write an expression for the left-hand side of Equation (2.56). The total force experienced by the fluid as it is sweeping through the fixed control volume is given by the sum of Equations (2.57) and (2.58) and Fviscous:

F=j^pfdV-^pdS + Fviscous [3.59]

v s

Now consider the right side of Equation (2.56). The time rate of change of momentum of the fluid as it sweeps through the fixed control volume is the sum of two terms:

Net flow of momentum out
of control volume across surface S

and

Consider the term denoted by G in Equation (2.60a). The flow has a certain momen­tum as it enters the control volume in Figure 2.17, and, in general, it has a different momentum as it leaves the control volume (due in part to the force F that is exerted on the fluid as it is sweeping through V). The net flow of momentum out of the control volume across the surface S is simply this outflow minus the inflow of momentum across the control surface. This change in momentum is denoted by G, as noted above. To obtain an expression for G, recall that the mass flow across the elemental area dS is (pV • dS); hence, the flow of momentum per second across dS is

(pV • dS)V

The net flow of momentum out of the control volume through S is the summation of the above elemental contributions, namely,

In Equation (2.61), recall that positive values of (pV • dS) represent mass flow out of the control volume, and negative values represent mass flow into the control volume. Hence, in Equation (2.61) the integral over the whole control surface is a combination of positive contributions (outflow of momentum) and negative contributions (inflow
of momentum), with the resulting value of the integral representing the net outflow of momentum. If G has a positive value, there is more momentum flowing out of the control volume per second than flowing in; conversely, if G has a negative value, there is more momentum flowing into the control volume per second than flowing out.

Now consider H from Equation (2.60b). The momentum of the fluid in the elemental volume dV shown in Figure 2.17 is

(,pdV)

The momentum contained at any instant inside the control volume is therefore

v

and its time rate of change due to unsteady flow fluctuations is

pVdV [2.62]

v

Combining Equations (2.61) and (2.62), we obtain an expression for the total time rate of change of momentum of the fluid as it sweeps through the fixed control volume, which in turn represents the right-hand side of Equation (2.56):

(mV) = G + H = <jlj> (pV • dS)V + Pv dV [2.63]

S V

Hence, from Equations (2.59) and (2.63), Newton’s second law,

d

— (mV) = F dt

applied to a fluid flow is

[2.64]

Equation (2.64) is the momentum equation in integral form. Note that it is a vector equation. Just as in the case of the integral form of the continuity equation, Equation

(2.64) has the advantage of relating aerodynamic phenomena over a finite region of space without being concerned with the details of precisely what is happening at a given distinct point in the flow. This advantage is illustrated in Section 2.6.

From Equation (2.64), we now proceed to a partial differential equation which relates flow-field properties at a point in space. Such an equation is a counterpart to the differential form of the continuity equation given in Equation (2.52). Apply

where the subscripts у and z on / and T denote the у and z components of the body and viscous forces, respectively. Equations (2.70a to c) are the scalar x, y, and г components of the momentum equation, respectively; they are partial differential equations that relate flow-field properties at any point in the flow.

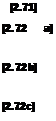Note that Equations (2.64) and (2.70a to c) apply to the unsteady, three-dimensional flow of any fluid, compressible or incompressible, viscous or inviscid. Specialized to a steady (d/dt = 0), inviscid (FviSCous = 0) flow with no body forces (f = 0), these equations become

Since most of the material in Chapters 3 through 14 assumes steady, inviscid flow with no body forces, we will have frequent occasion to use the momentum equation in the forms of Equations (2.71) and (2.72a to c).

The momentum equations for an inviscid flow [such as Equations (2.72a to c)] are called the Euler equations. The momentum equations for a viscous flow [such as Equations (2.70a to c) are called the Navier-Stokes equations. We will encounter this terminology in subsequent chapters.